I. 서 론
창의적 사고력은 양적인 차원에서 새롭고 유용한 아이디어를 생성함과 동시에 질적인 차원에서 아이디어를 잘 선택하는 인지 능력을 의미한다(Lee & Therriault, 2013). 이러한 창의적 사고력은 로봇이나 인공지능이 가질 수 없으며, 인간만이 가지는 고유한 고차원적 능력으로 여겨지며 교육 현장에서 주목을 받고 있다(김유중, 이선영, 2021). 또한 사회적으로 여러 가지 학문 분야 간의 경계를 허물어 창의적이고 융합적으로 사고하는 유연한 인재를 요구하고 있는 상황에서 교육 영역에서의 창의적 사고력은 더욱 강조되고 있는 역량이라고 할 수 있다(신소영, 이승희, 2017). 이러한 창의적 사고력은 개인의 보유하고 있는 고정된 능력이 아니라 교육이나 훈련을 통해 충분히 계발할 수 있다는 점에서 교육적인 의미가 있다고 할 수 있다(Sun, Wang, & Wegerif, 2019). 이러한 교육적인 의미를 바탕으로 우리나라 2015 개정 교육과정에서는 창의・융합형 인재 양성을 위해 창의적 사고역량을 핵심역량 중 하나로 선정하였다(교육부, 2015). 2022 개정 교육과정에서도 창의성 교육의 중요성을 지속적으로 강조하며 창의적 사고역량을 핵심역량으로 유지하였다(교육부, 2022). 뿐만 아니라 OECD(2018)에서 제시한 ’Education 2030’에서는 미래 사회에 필요한 역량 중 하나로 새로운 가치 창조하기를 제안하며 창의적인 사고를 강조하였다. 이에 OECD에서 시행하는 PISA(Programme for International Student Assessment) 2022에서는 지능사회를 살아갈 학생들이 갖추어야 할 역량이라는 점을 강조하여 혁신적 영역으로 창의적 사고력을 포함하여 전 세계 청소년의 창의적 사고력을 평가하였다(교육부, 2024; 조성민 외, 2019).
창의성을 창의적 사고와 창의적 성격으로 구분할 때, 창의적 사고는 창의성의 확산적, 인지적 영역을 다루고 창의적 성격은 정의적 영역을 다룬다고 할 수 있다(김진우, 박혜성, 이선영, 2020). PISA 2022에서도 창의적 사고력을 창의적 작업에 참여하는 데 필요한 인지적 과정에 주안점을 두었다는 점에서 연습을 통해 증대시킬 수 있으며 일상적인 맥락에서 합리적으로 입증할 수 있는 능력이라고 보았다(김성경 외, 2024; OECD, 2024a). 이처럼 PISA 2022에서 측정하고자 하는 창의적 사고력은 학습과 교육을 통해 증대시킬 수 있다는 점(김현우, 2024)에서 평가 결과를 통해 학생들의 창의적 사고력을 높일 수 있는 방안을 마련할 수 있을 것이다.
한편, 학습자의 현재 수준을 파악하여 적절한 교육을 제공하기 위한 중요한 척도로서 평가 결과를 활용하기 위해서는 타당한 검사도구의 선택과 활용이 우선적으로 요구된다(윤지영, 이윤선, 2013). 이에, 검사의 타당도를 검정하기 위한 하나의 방법으로 차별기능문항을 탐색하는 연구가 심리 측정 평가와 검사 개발 영역에서 중요하게 다루어지고 있다(안선영, 2022).
차별기능문항은 동일한 수준의 능력을 가진 피험자들이 집단 특성으로 인해 검사 문항에 반응이 달라지는 것을 의미하며 검사의 공정성 측면에서 매우 중요한 요소이다(장윤선, 이주연, 2023; Holland & Wainer, 2012). 평가는 학습자의 능력을 정확하게 측정해야 하고 특정 집단에 따라 편파 없이 공정하게 이루어져야 하기 때문에 대규모로 이루어지는 표준화 검사에서 중요한 고려사항이라고 할 수 있다(서경숙, 안해연, 최윤정, 2024). 이에 국내외에서 시행되는 대규모 표준화 검사에 대해 차별기능문항을 탐색하는 선행연구가 이루어져 왔다. 국내에서 이루어진 선행연구를 먼저 살펴보면 서민철(2013)은 국가수준 학업성취도 평가의 사회과 문항에 대한 ‘지역규모’에 따른 차별기능문항을 탐색하였으며, 김종민, 이문수, 안성훈(2016)은 국가수준 ICT 리터러시 검사에 대해 ‘성별’에 따른 차별기능문항을 탐색하였다. 또한 차별기능문항을 탐색하는 선행연구가 PISA(고수경, 2024; 노언경, 김진호, 김수진, 2010; 박정, 2010; 손원숙, 2010; 장윤선, 이주연, 2023; Kucam & Gülleroǧlu, 2023; Zeybekoǧlu, Güneş, Yalçın, 2024), TIMSS(Trends in Mathematics and Science Study)(권승아, 2018; 서경숙, 안해연, 최윤정, 2024; 윤지영, 이윤선, 2013), ICILS(International Computer and Information Literacy Study)(이문수, 2018) 등 국제 학업성취도 평가에 적용하여 이루어지고 있다.
한편, 차별기능문항을 탐색한 대부분의 선행연구에서는 제한된 변인을 활용하여 집단을 구분하고, 집단 간 차별기능문항을 탐색하여 왔다. 대표적으로, ‘성별’ 간 차별기능문항을 탐색하거나(권승아, 2018; 김종민, 이문수, 안성훈, 2016; 노언경, 김진호, 김수진, 2010; 박정, 2006), 국가(손원숙, 2010; 윤지영, 2013; 이문수, 2018), ‘지역규모’(서민철, 2013), ‘디지털 기기 친숙도’(서경숙, 안해연, 최윤정, 2024)를 기준으로 하위집단을 구분하여 차별기능문항을 탐색해 왔다. 이처럼 차별기능문항을 탐색하는 전통적인 방법은 하위집단을 사전에 설정해야만 적용할 수 있다는 한계를 가진다. 그러나 연구자가 관심에 따라 제한된 일부의 변인을 활용하여 사전에 하위집단을 구분하는 것은 자료에 포함된 다양한 특성을 반영할 수 없다는 점에서 차별기능문항을 탐색하여 검사의 공정성을 확보하는데 충분하지 않을 수 있다(장윤선, 이주연, 2023).
차별기능문항 탐색에 있어 이러한 전통적인 접근법의 한계점을 보완하고자 기계학습 기반의 재귀적 자료 분할 기법의 방법이 제안되었다. Rasch 모형을 기반으로 하는 Rasch tree 방법은 자료에서 활용할 수 있는 여러 설명변인의 조합을 바탕으로 정의될 수 있는 하위집단에 대한 반복적인 통계검증을 통해 차별기능문항을 탐색하는 방법이다(Strobl, Kopf, & Zeileis, 2015). Rasch tree 방법은 연구자의 관심에 따라 제한된 정보를 활용하여 사전에 하위집단을 설정하여(예, 성별, 지역) 차별기능문항을 탐색하는 방법에서 벗어나 분석자료에 포함된 다양한 설명변인을 활용하여 도출된 잠재집단을 하위집단으로 정의한다는 점에서 전통적인 방법과 차이를 가진다(장윤선, 이주연, 2023). 또한 Rasch tree는 자료에서 활용할 수 있는 설명변인을 바탕으로 차별기능문항을 탐색하고 그 원인을 확인하는 것을 동시에 수행할 수 있다는 장점을 가져 다양한 설명변인을 활용할 수 있을 뿐만 아니라 의사결정나무 기반 알고리즘을 적용하여 결과를 나무구조로 표현하여 결과를 직관적으로 해석할 수 있다는 장점을 가진다(장윤선, 이주연, 2023). 이에 본 연구에서는 학생, 학부모를 대상으로 한 설문조사를 바탕으로 PISA 2022에 포함된 다양한 설명변인을 활용하여 Rasch tree 방법을 통해 PISA 2022 창의적 사고력 영역의 차별기능문항을 탐색하고, 차별기능을 유발하는 변인을 파악하고자 한다. 이를 통해 PISA 2022 창의적 사고력 영역이 학생들의 창의적 사고력을 타당하고 공정하게 평가하는지를 파악하고, 차별기능문항이 발생하는 원인과 특성에 대해 보다 많은 정보를 제공하고자 한다. 이러한 목적을 위해 설정한 본 연구의 연구문제는 다음과 같다.
II. 이론적 배경
창의성에 대한 다양한 연구가 이루어지고 있지만, 창의성을 확산적 사고로 강조하는 측면과 정의적 특성을 강조하는 측면으로 크게 구분할 수 있다(김진우, 박혜성, 이선영, 2020). 확산적 사고는 주어진 자극에 대해 다양한 범위의 아이디어를 생성하는 과정을 의미한다(김유중, 이선영, 2021). 이는 Kaufman(2009)이 제안한 창의성을 이해하는 접근 방식 중 하나인 3Ps(사람, 과정, 결과물) 중 ‘과정(Process)’에 해당하며, 창의성이 발현되고 계발되는 인지적 사고 과정에 중점을 두고 있음을 알 수 있다.
또한 Torrance(1965)는 창의성의 과정에 주목하며, 창의적 사고를 어려운 문제를 직면했을 때 문제를 해결하기 위해 적절한 질문을 할 수 있는 능력, 문제해결을 위한 예측 또는 가설을 세울 수 있는 능력, 설정한 예측이나 가설을 검증하고 적절한 해결 방법을 이끌어내는 능력으로 정의하였다. 창의적 사고는 창의성의 확산적 사고에 중점을 두어 인지적인 특성을 강조하고 있다고 할 수 있다(정미선, 정세영, 2010). 창의성을 연구하는 데 있어 비인지적, 정의적 측면을 살펴보는 것도 중요하지만, 주로 창의성을 설명하는 근본은 인지적인 측면을 강조하는 창의적 사고력이라고 평가되고 있다(Sun, Wang, & Wegerif, 2019).
Torrance(1970: 강윤정, 이순묵, 2010에서 재인용)는 창의성의 핵심 요소로 확산적 사고를 제시하며, 이를 구성하는 네 가지 하위요인으로 유창성, 유연성, 독창성, 정교성을 제안하였다. 유창성은 얼마나 많은 아이디어를 생성하는가에 관한 내용이며, 유용성은 시대와 상황에 맞는 실용적인 아이디어를 생성하는가에 대한 내용이다. 독창성은 새롭고 독특한 아이디어인가를 의미하며 정교성은 아이디어를 정제하여 구체화하는가에 대한 내용이다(황지영, 이선영, 2021). 한국교육개발원에서 수집한 학생역량 조사도구에서는 창의적 사고역량을 창의적 사고와 관련된 발산적 사고력, 독창적 유연성, 창의적 성향과 관련된 모험심, 탐구심 4개의 하위요인으로 구성하였다(남궁지영 외, 2015). 이 중 창의적 사고와 관련된 발산적 사고력은 하나의 문제에 여러 가지 답을 제시할 수 있는 능력을 의미하며(김위정, 이혜정, 김태기, 2014), 독창적 유연성은 일상생활에 필요한 참신하고 독특한 아이디어를 생성하는 것을 의미한다(정은이, 박용한, 2002).
한편, 혁신적 영역에서 창의적 사고력을 측정한 PISA 2022에서는 창의적 사고력을 창의적 작업에 참여하는 데 필요한 인지적 과정에 중점을 두고, 교육을 통해 이를 증대시키며 일상에서 입증할 수 있는 능력으로 정의하였다(김성경, 2024; OECD, 2024a). 이를 위해 PISA는 창의적 사고력을 아이디어 형성과정과 영역 두 가지 차원으로 구분하여 측정하고자 하였다. 아이디어 형성과정 차원에서는 ‘다양한 아이디어 만들기’, ‘독창적 아이디어 만들기’, ‘아이디어 평가하고 개선하기’로 구분하였으며, 영역 차원에서는 ‘문어 표현’, ‘시각 표현’, ‘사회적 문제 해결’, ‘과학적 문제 해결’로 구분하였다. 이를 통해 PISA는 창의적 사고력을 독창적이고 효과적인 문제 해결 방안과 표현으로 이어질 수 있는 아이디어의 생성, 평가 및 개선 과정에 참여하는 다차원적 역량으로 정의하였다(김성경 외, 2024; OECD, 2024a).
PISA 2022에서 측정하고자 하는 창의적 사고력은 일상생활에서 보여줄 수 있는 학생들의 역량을 의미한다(김현우, 2024). 실생활에서 접할 수 있는 다양한 문제에 대해 이를 해결할 아이디어를 생성하고 효과적인 문제 해결 방안을 도출하는 과정에서 나타날 수 있는 창의적 사고력은 여러 배경 변인에 의해 영향을 받을 수 있다. 이러한 배경 변인이 창의적 사고력에 미치는 영향을 고려할 때, 특정 변인에 따른 집단에 편향되지 않도록 정확하게 측정하고 파악하는 것이 중요하다(노언경, 김진호, 김수진, 2010). PISA 2022의 창의적 사고력은 학습과 교육을 통해 증대시킬 수 있다는 점(김현우, 2024)에서, 평가 결과를 바탕으로 창의적 사고력 향상 방안을 마련할 수 있다. 그러나 검사의 공정성 측면에서 문제가 발생할 경우, 적절한 방안을 마련하는 데 어려움을 초래할 수 있다. 이에 본 연구에서는 PISA 2022 창의적 사고력 영역에 대한 차별기능문항을 탐색하고 이를 유발하는 변인을 확인하여 검사의 공정성 측면에서 도움이 될 수 있는 정보를 제공하고자 한다.
차별기능문항은 동일한 수준의 능력을 가진 피험자들이 집단 특성으로 인해 검사 문항에 반응이 달라지는 것을 의미하며 검사의 공정성에 있어 매우 중요한 요소이다(장윤선, 이주연, 2023; Holland & Wainer, 2012). 이에 차별기능문항의 여부를 확인하는 것은 검사의 공정성과 타당성을 확보하는데 기본 전제가 되어야 하는 과정이라고 할 수 있다(Camilli & Shepard, 1994; Clauser & Mazor, 1998). 차별기능문항은 검사의 공정성 차원에서 중요한 문제로 인식되어 국내외에서 차별기능문항을 탐색하는 연구가 수행되어 왔다(김종민, 이문수, 안성훈, 2016). 차별기능문항이 존재하여 특정 집단에 편향되고 공정하지 못한 검사가 이루어진다면 평가 결과를 바탕으로 피험자의 특성을 정확하게 파악할 수 없기 때문에 이는 대규모 표준화 검사를 이용한 평가에서 중요한 고려사항 중 하나이다(서경숙, 안해연, 최윤정, 2024).
국제 학업성취도 평가는 여러 국가의 학생들을 대상으로 동일한 기준으로 진행되기 때문에, 평가 결과의 공정성을 확보하기 위해 차별기능문항 탐색이 필수적이다. 이에 따라, 국제 학업성취도 평가에서 차별기능문항을 탐색하고 개선하려는 연구가 지속적으로 이루어지고 있다. 먼저, 4학년과 8학년을 대상으로 수학, 과학 성취도 추이변화 국제 비교를 위한 TIMSS와 관련된 선행연구를 살펴보면, 윤지영, 이윤선(2013)의 연구에서 TIMSS 2007 8학년 수학 교과에 대해 SIBTEST(Simultaneous Item Bias Test)(Shealy & Stout, 1993) 방법을 적용하여 국가(한국, 미국, 싱가폴)에 따른 차별기능문항을 탐색한 결과, 한국과 미국 간의 비교에서 한국 학생에게 20개 문항, 미국 학생에게 21개 문항이 유리한 것으로 나타났으며, 한국과 싱가폴 간의 비교에서는 한국 학생에게 31개 문항, 싱가폴 학생에게 17개 문항이 유리한 것으로 나타났다. 권승아(2018)은 TIMSS 2015 8학년 수학 교과에 대해 인지진단모형 기반의 CDM(Cognitive Daianosis Model)-Wald 검정(Hou, de la Torre & Nandakumar, 2014)과 LCDM(LogLinear Cognitive Diagnosis Model)-DIF 방법(Li & Wang, 2015)을 적용하여 한국 학생의 ‘성별’에 따른 차별기능문항을 탐색한 결과 각 방법에서 5개 문항이 차별기능문항으로 추출되었으며 공통적으로 3개의 차별기능문항이 존재한다고 보고하였다. 서경숙, 안해연, 최윤정(2024)의 연구에서는 컴퓨터 기반으로 실시된 eTIMSS 2019 4학년 수학 교과에 대해 로지스틱 회귀분석, Mantel-Haenszel 방법(Holland & Thayer, 1988), IRT 우도비 검정 방법(Thissen, Steinberg & Wainer, 1988)을 활용하여 한국 학생을 대상으로 ‘디지털 기기 친숙도’가 높은 집단과 낮은 집단 간의 차별기능 문항을 탐색하였다. 탐색 결과, PSI(Problem Solving and Inquiry) 문항 중 10개의 차별기능이 존재하는 것으로 나타났다. 이문수(2018)의 연구는 8학년을 대상으로 국제 컴퓨터・정보 소양을 연구하는 ICILS 2013에 대해 국가별(한국, 노르웨이, 폴란드) 및 ‘성별’에 따른 차별기능문항을 Wald-test(Wald, 1943)를 통해 탐색한 결과, 유럽 국가 학생의 경우 남학생에게 9개 문항, 여학생에게 7개 문항이 유리하였으며, 한국의 경우 남학생에게 유리한 1개 문항, 여학생에게 유리한 3개 문항이 존재하는 것으로 나타났다.
PISA와 관련된 연구들은 다양한 영역에서 차별기능문항 탐색이 수행되었는데, 박정(2006)은 PISA 2003의 과학 영역에서 한국 학생의 ‘성별’에 따른 차별기능문항을 다집단 문항반응이론 모형을 적용하여 탐색한 결과, 남학생에게 유리한 12개 문항이 발견되었다고 보고하였다. 노언경, 김진호, 김수진(2010)은 PISA 2003의 문제해결력 영역의 차별기능문항을 한국 학생의 ‘성별’에 따라 탐색하였는데, 균일적 차별기능 탐색을 위해 Mantel-Haenszel 방법, SIBTEST 방법, 문항 난이도 모수 비교 방법을 활용하였으며, 비균일적 차별기능 탐색을 위해 로지스틱 회귀분석, Crossing SIBTEST(Li & Stout, 1996), Raju 방법(Raju, 1988), IRT 우도비 검정을 활용하였다. 이에 각각 5개의 균일적, 비균일적 차별기능문항이 나타났으며 3개의 문항이 네 가지 이상의 방법에서 차별기능문항으로 나타났다. 장윤선, 이주연(2023)의 연구에서는 한국 학생을 대상으로 Rasch tree 방법을 통해 PISA 2015 과학 영역의 차별기능문항을 탐색한 결과, ‘과학의 즐거움’, ‘성별’, ‘과거 과학 활동 경험’ 변인에 의해 2개의 차별기능문항이 나타났음을 확인하였다. 또한, Zeybekoǧlu, Güneş, Yalçın(2024)의 연구에서는 PISA 2018 읽기 영역에 대해 ‘성별’, ‘학교위치’, ‘ESCS’에 의한 차별기능문항을 Mantel-Haenszel, 로지스틱 회귀분석, SIBTEST, Raju 방법을 활용하여 탐색한 결과, ‘성별’은 방법에 따라 2~7개, ‘ESCS’는 1~15개 문항의 차별기능문항이 나타났다. Kucam, Gülleroǧlu(2023)은 튀르키예 학생을 대상으로 PISA 2018 수학 영역에 대해 ‘성별’과 ‘부모교육수준’에 따른 차별기능문항을 Mantel-Hanszel 방법, 로지스틱 회귀분석, Rasch tree 방법을 적용하여 탐색한 결과, 세 방법에서 공통적으로 여학생에게 유리한 3개 문항이 확인되었다. 국제 학업성취도 평가에 대해 차별기능문항을 다양한 방법을 활용하여 탐색한 많은 선행연구에서 차별기능문항이 존재하는 것으로 나타났다. 국제 학업성취도 평가는 각 국가 청소년 성취 수준과 심리 상태를 측정하고 국제적 비교를 통해 교육 정책을 도출하는 데 활용된다는 점에서 검사 도구의 타당성을 면밀히 검토할 필요가 있다.
국제학업성취도 평가의 차별기능문항을 탐색하는 선행연구에서는 차별기능을 유발하는 집단을 사전에 설정하기 때문에 연구자에 의해 하위집단이 정의된다는 점에서 검사도구의 공정성 확보에 충분하지 않을 수 있다(장윤선, 이주연, 2023). 또한, 범주형 변인을 활용하여 집단을 구분하거나 연속형 변인의 경우 특정 값을 기준으로 하위집단을 사전에 설정해야 하는데(Geramipour, 2020), 연속형 변인을 활용하여 하위집단을 설정하는 경우 기준값 설정이 어려움이 있으며, 이를 범주형 변인으로 변환하는 과정에서 본래 가지고 있던 정보가 손실될 수 있다(장윤선, 이주연, 2023). 또한, 최근 다양한 설명변인이 포함된 자료가 제공되고 있다는 점에서, 사전에 하나의 변인을 바탕으로 하위집단을 구분하는 방식은 차별기능문항이 나타나는 원인을 탐색하는 데 충분하지 않을 수 있다. 이러한 한계를 극복하기 제안된 Rasch tree 방법은 기계학습을 기반으로 하는 재귀적 자료 분할 기법으로, 문항반응이론의 Rasch 모형을 통계적 기반으로 활용하는 방법이다(Strobl, Kopf, & Zeileis, 2015). Rasch tree 방법은 자료에 포함된 설명변인의 조합을 바탕으로 정의될 수 있는 하위집단에 대해 반복적인 통계검증을 통해 차별기능문항을 탐색하는 방법이다. 이 과정에서 하위집단 간 난이도 차이가 있는 경우 자료를 분할하고, 자료가 분할되지 않을 때까지 반복하여 차별기능문항을 탐색한다(Strobl, Kopf, & Zeileis, 2015). 또한, Rasch tree 방법은 설명변인을 통해 차별기능문항을 탐색하고 그 원인을 확인하는 분석을 한 번에 수행할 수 있을 뿐만 아니라, 의사결정나무 기반의 알고리즘을 적용하여 분석 결과를 나무구조로 시각화함으로써 차별기능문항 탐색 결과를 직관적으로 해석할 수 있다는 장점이 있다(장윤선, 이주연, 2023). 이러한 점에서, 자료에 포함된 설명변인의 조합을 바탕으로 하위집단을 구분하는 Rasch tree 방법은 성취도뿐만 아니라 다양한 설명변인을 포함하고 있는 PISA 2022 자료에서 차별기능문항을 탐색하는 데 적합한 방법이라고 할 수 있다.
Rasch tree 방법을 활용한 차별기능문항 탐색은 크게 문항 모수 추정, 문항 모수에 대한 불안정성 평가, 자료 분할의 세 단계로 구분할 수 있으며 이러한 과정을 반복하여 이루어진다(고수경 외, 2024; Strobl, Kopf, & Zeileis, 2015). 첫 번째 단계는 문항 모수를 추정하는 단계로 문항에 대한 응답 자료를 바탕으로 Rasch 모형의 문항 모수를 조건부최대우도추정법(Conditional Maximum Likelihood Estimation; CMLE)을 적용하여 추정한다. Rasch 모형의 문항 모수를 추정하는 식은 다음과 같다.
위 식에서 yij는 피험자 i의 문항 j에 대한 이분형 문항 반응이고 βj는 문항 j에 대한 난이도를, θi는 피험자 i의 능력모수를 의미한다.
두 번째 단계는 문항 모수의 불안정성 평가로 첫 번째 단계에서 추정한 문항 모수가 설명변인에 따라 유의한 차이가 있는지를 확인하는 단계이다. 이를 위해 추정된 문항 모수를 통해 개별 점수를 산출하고 설명변인에 따라 정렬하여 구조적인 변화를 확인한다. Rasch 모형을 기반으로 개별 점수를 산출하는 식은 다음과 같다.
위 식에서 yi는 피험자 i의 응답을 의미하며, β는 문항 모수, ri는 피험자 i의 관찰된 원점수를 의미한다. 이를 통해 계산된 개별 점수가 설명변인의 값에 따라 체계적인 변화 양상이 나타난다면 차별기능문항이 존재한다는 것을 의미하며, 설명변인의 값에 상관없이 무선적인 양상이 나타난다면 차별기능문항이 존재하지 않는다는 것을 의미한다. 이러한 개별 점수와 설명변인 간에 나타나는 특정한 관계는 개별 점수 누적 함수를 통해서도 확인할 수 있다. 추정된 문항 모수가 특정 설명변인과 상관없이 안정적이라면 개별 점수 누적 함수의 평균이 0이 되는 무선적인 분포를 보이며, 불안정하다면 특정한 양상을 가지는 분포를 보여 차별기능문항이 존재한다는 것을 의미한다. 개별 점수 누적 함수를 산출하는 식은 다음과 같다.
위 식에서 y(i|l)는 전체 자료를 연속형 설명변인 l을 기준으로 오름차순으로 정렬했을 때, i번째에 해당하는 피험자의 문항에 대한 반응을 의미한다. n은 전체 피험자 수를, t는 설명변인의 값에 따라 분할되는 피험자의 비율, ⌊n×t⌋는 n × t의 정수 부분 값을 의미한다.
세 번째 단계는 자료 분할 단계로 두 번째 단계에서 나타난 문항 모수의 불안정도가 통계적으로 유의하다면 이는 차별기능문항이 존재한다는 것을 의미한다. 따라서 문항 모수의 불안정도가 가장 높은 설명변인을 선택하여 자료분할이 이루어진다. 선택된 설명변인이 이분변인이라면 범주에 따라 자료가 분할되며, 연속형 변인 또는 세 개 이상의 범주를 가지는 변인의 경우 설명변인에 의해 분할되는 자료의 분할된 로그우도가 최대가 되는 값을 기준점으로 하여 자료를 분할한다. 자료 분할의 기준점을 산출하는 식은 다음과 같다.
위 식에서 L(ξ) = {i|xil ≤ ξ}은 나무구조에서 분할된 자료의 한쪽 가지에 해당하는 부표본을 의미하며 R(ξ) = {i|xil ≤ ξ}은 다른 가지의 부표본을 의미한다. 와 은 분할된 자료에 대해 추정된 Rasch 모형의 문항 모수를 의미한다. 위 식을 통해 산출된 로그우도에 대한 우도비 검증을 통해 모형의 적합도가 가장 크게 향상되는 값을 자료 분할의 기준점으로 설정한다. 세 번째 단계에서 분할된 부표본에 대해 다시 문항 모수를 추정하고, 이에 대한 불안정도를 평가한 후 자료 분할을 반복하게 된다. 이를 자료가 분할되지 않을 때까지 반복하여 차별기능문항을 탐색한다.
III. 연구방법
본 연구는 2022년에 시행된 PISA 본검사 자료 중 만 15세 한국 학생의 창의적 사고력 검사에 대한 응답자료를 활용하였다. PISA에서는 학생들의 삶에 대한 준비도를 포괄적으로 전망하기 위해 혁신적 영역을 매 주기 선정하여 평가하고 있다(교육부, 2024). PISA 2022의 혁신적 영역은 창의적 사고력으로 본 연구에서는 창의적 사고력 영역에 응시한 1,713명(남 868명, 여 845명)을 대상으로 하였다.
PISA 2022 본검사의 창의적 사고력 영역은 총 32문항(문어 표현 12문항, 시각 표현 4문항, 사회적 문제 해결 10문항, 과학적 문제 해결 6문항)으로 구성되었다. PISA 2022 본검사 대상으로 표집된 학생들은 모든 문항에 응답하지 않고 무작위로 할당된 소검사에 따라 일부 문항에 응시하게 된다는 점에서 학생들이 응답한 문항에 따라 5개의 자료로 구분하였다. 또한, OECD에서는 창의적 사고력 영역을 측정하기 위해 32개 문항을 개발하여 검사를 시행하였으나(OECD, 2024a), 공개된 자료에서는 우리나라의 경우, 1개 문항(T360Q01)이 제외되었기 때문에, 본 연구에서는 최종 31개 문항을 분석에 활용하였다(김성경 외, 2024). 창의적 사고력 문항은 모두 개방형 문항으로 채점을 통해 점수가 부여되며 31문항 중 4문항은 오답인 경우 0점, 정답인 경우 1점인 이분형 문항이며, 나머지 문항은 부분점수를 가지는 다분형 문항으로 구성되어 있다. 각 자료별 문항에 대한 정보와 대표 문항의 내용 및 응시 인원수는 <표 1>과 같다.
b) 김성경 외(2024)에서 발췌함
c) OECD(2024a)에서 발췌함
PISA에서는 성취도 검사뿐만 아니라 학생, 학부모, 교사를 대상으로 설문을 실시하였다. Rasch tree 방법을 통해 창의적 사고력 영역의 차별기능문항을 탐색하기 위해 선행연구(고수경, 2024; 장윤선, 이주연, 2023)를 참고하여 학생의 성취와 관련이 있을 것으로 고려되는 학생 및 학부모 설문자료를 분석에 포함하였다. Rasch tree 분석에 있어 자료의 전체적인 구조를 고려하여 설명변인의 자료 분할 기준값을 결정한다는 점(Strobl, Kopf, & Zeileis, 2015)에서 설명변인을 연속형 변인과 이분범주형 변인으로 한정하였다. 이를 통해 67개의 설명변수를 선정하였으며 학생 개인 특성 13문항, 부모 및 가정 특성 11문항, 학교 특성 5문항, 수학 역량 특성 14문항, ICT 영역 16문항, 창의적 사고력 관련 태도 및 환경 8문항으로 구성되었다. PISA에서는 설명변수 중 일부를 설문문항을 변환하거나 척도화하여 새롭게 생성한 파생변수로 제공한다. 이는 설명변수의 잠재적인 특질 추정을 위해 가중 우도 추정치(Weighted Likelihood Estimates: WLE)를 사용하여 생성한다(OECD, 2023). 가중 우도 추정치를 통해 생성된 설명변수는 OECD 국가 전체에 대해 평균 0, 표준편차 1로 표준화한 값을 기준으로 한다. 즉, 0보다 작은 경우 OECD 평균보다 낮다는 것을 의미하며, 0보다 크면 OECD 평균보다 높다는 것을 의미한다(OECD, 2024b). PISA 2022 설명변수 중 가중 우도 추정치를 통해 생성된 파생변수가 있는 경우 파생변수를 분석에 활용하였으며, 파생변수가 없는 경우 개별문항 또는 하위문항의 평균을 활용하였다. 분석에 활용된 PISA 2022 설명변인은 <표 2>와 같다.
| 구분 | 변인 | |
|---|---|---|
| 설명 변인 | 학생(13) | 성별a), 등교전/방과후 스포츠 활동 빈도b), 등교전/방과후 학습 활동 빈도c), 유아 교육 및 보육 기간d), 학생이 기대하는 직업 지위, 인내심e), 호기심e), 협력e), 공감e), 자기 주장e), 스트레스 저항력e), 정서 조절e), 자기주도학습에 대한 효능감e) |
| 부모 및 가정(11) | 가족의 지원e), 모 교육수준f), 부 교육수준f), 가정에서 보유한 도서 수e), ESCSe), 학부모 지원e), 학교 활동 참여도e), 창의적 가정환경e), 학교 밖 창의적 활동 참여e), 부모의 창의성과 지적 개방성e), 자녀의 창의적 개방성e) | |
| 학교(5) | 학생-교사관계의 질e), 학교 소속감e), 따돌림 경험e), 학교 안전감e), 학습 지속을 위한 학교의 지원 활동e) | |
| 수학 역량 특성(14) | 타 교과 대비 수학 선호도g), 수학에 대한 쉬움 인식h), 수학에 대한 동기 부여i), 수학 수업의 분위기e), 수학 교사의 지원e), 수학 인지 활성화: 추론 능력 함양e), 수학 인지 활성화: 수학적 사고 함양e), 형식적/응용 수학 과제 노출e), 수학 추론 및 21세기 수학 주제 노출e), 수학 자기효능감: 형식적 수학과 응용 수학e), 수학 자기효능감: 추론과 21세기 수학e), 수학 개념 친숙도e), 수학 불안e), 수학 학습에 대한 노력과 끈기e) | |
| ICT 영역(16) | 학교에서의 일상적인 ICT 사용e), 학교에서 ICT 사용 접근성j), 학교 밖에서의 ICT 사용e), 가정에서 ICT 사용 접근성k), 수업에서 주제와 관련된 ICT 사용e), 수업 이외의 주제와 관련된 ICT 사용e), ICT를 활용한 학습지원e), ICT를 활용한 교내 활동e), 주중 여가 활동에서 ICT 활용 시간e), 주말 여가 활동에서 ICT 활용 시간e), 학교에서 ICT 사용에 대한 의견e), 디지털 역량에 대한 자기 효능감e), ICT를 활용한 수학 활동, 컴퓨터 프로그래밍에 대한 흥미, 디지털 기기 사용 시간, 디지털 기기 활용 행동 | |
| 창의적 사고력 관련 태도 및 환경(8) | 창의적 사고력 효능감e), 창의적 학교 및 수업 환경e), 창의적 또래 및 가정 환경e), (교내) 창의적 활동 참여e), (교외) 창의적 활동 참여e), 창의성과 지적 개방성e), 예술적 개방성e), 상상력과 모험심e) | |
| ※ 주 변수명은 PISA 설명변인 관련 선행연구(김성경 외, 2023; 김성경 외, 2024; 정혜원, 박소영, 2022; 조성민 외, 2019)를 참고하여 작성함(이탤릭: 개별문항, 진하게: 하위문항 평균, 이외 변수는 WLE 변인 활용) | ||
본 연구는 PISA 2022 창의적 사고력 영역의 차별기능문항을 탐색하기 위해 Rasch tree 방법(Strobl, Kopf, & Zeileis, 2015)을 분석에 활용하였다. 먼저 PISA는 표집된 학생들에게 전체 문항 중 일부를 무작위로 할당하는 검사로 설계되었다(신효정, 2021). 이러한 검사 설계에 따라 학생들은 창의적 사고력 영역의 모든 문항에 응답하지 않으며, 학생마다 할당된 일부 문항에만 응답하게 된다. 이에 따라 본 연구에서는 한국 학생들의 창의적 사고력 응답자료를 응답한 문항에 따라 5개의 자료로 구분하였다. 또한, Rasch tree 방법을 적용하기 위해 31개 문항 중 다분형 문항 27개 문항에 대해 선행연구(고수경 외, 2024)를 참고하여, 점수를 받지 못하였거나(0), 부분점수를 받은 경우(1)는 0으로, 정답인 경우(2)는 1로 재코딩하였다.이 과정에서 자료별로 모든 문항에 응답하지 않은 경우는 분석에서 제외하였다. Rasch tree 방법을 적용하기 위해 자료별로 문항에 대한 응답값이 행렬구조를 가진 하나의 종속변인으로 설정해야 하기 때문에(Strobl et al., 2021) 자료별로 2-8개의 문항에 대한 응답을 하나의 종속변인으로 설정하였다. 설명변인은 학생 및 학부모 설문을 통해 변환된 파생변수와 개별문항 및 하위문항 평균값을 전처리하여 투입하였다. 설명변인에 대한 결측값은 R 프로그램(Ver. 4.2.2)의 mice(Ver, 3.17.0) 패키지(van Buuren & Groothuis–Oudshoorn, 2011)를 활용하여 1회 대체하였다.
본 연구에서는 Rasch tree 방법 적용에 있어 추정된 문항 모수의 불안정성 평가의 통계적 검증 기준을 유의수준 5%로 설정하여 자료 분할을 반복하였다. 이를 통해 각 자료에 대해 분할된 나무구조를 통해 차별기능을 유발하는 설명변인이 무엇인지와 기준점을 확인하였다. 한편, 차별기능문항 결과 해석을 위하여, 도출된 설명변인의 기준점에 의해 분할된 하위집단별 난이도의 차이의 기준을 장윤선, 이주연(2023)의 연구를 참고하여 1로 설정하였다. 이를 위해 R 프로그램(Ver. 4.2.2)을 활용하였으며 psychotree 패키지(Ver. 0.16-1)에 포함된 raschtree 함수를 활용하였다.
Rasch tree 방법은 추정된 문항 모수에 대한 신뢰구간을 제공하지 않기 때문에 하위집단별 문항 모수의 통계적인 차이를 확인할 수 없다. 이에 Rasch tree 분석 결과에 대한 안정성 평가를 실시하였다. 안정성 평가는 분석에 활용한 자료에 대한 재표집을 통해 Rasch tree 분석을 반복적으로 실시하여 원 자료에 대한 분석결과와 일치하는지를 확인하였다. 안정성 평가를 위해 R 프로그램(Ver. 4.2.2)의 stablelearner 패키지(Ver. 0.1-5)에 포함된 stabletree 함수를 활용하였다. 이때 재표집의 표본 크기와 반복분석 횟수는 Rasch tree 결과에 대한 안정성 평가를 수행한 선행연구(장윤선, 이주연, 2023; Strobl et al., 2021)을 참고하여 전체 자료의 63.2%와 500회로 설정하였다.
IV. 연구결과
본 연구에서는 PISA 2022 창의적 사고력 영역의 차별기능문항을 탐색하기 위해, 우리나라 학생들의 창의적 사고력 응답자료와 설문자료에 Rasch tree 방법을 적용하여 차별기능문항을 탐색하고, 이를 유발하는 변인을 확인하였다. 학생들이 응시한 문항에 따라 A부터 E까지의 5개 자료로 구분하여 분석을 실시하였으며, 이 중 문항 수가 2개로 적어 분석 결과가 도출되지 않은 자료 E를 제외한 4개 자료에 대한 결과를 제시하였다. 먼저, 자료 A의 8개 문항에 대한 차별기능문항 탐색 결과를 나무구조로 표현하면 [그림 1]과 같으며, 한 번의 자료 분할을 통해 2개의 하위집단이 도출되었다. 이 자료 분할은 학교 관련 설명 변인인 ‘학교 소속감’에 의해 이루어졌으며, 기준점은 –0.61로 나타났다. 하위집단별 각 문항의 추정난이도는 <표 3>에 제시되어 있다.
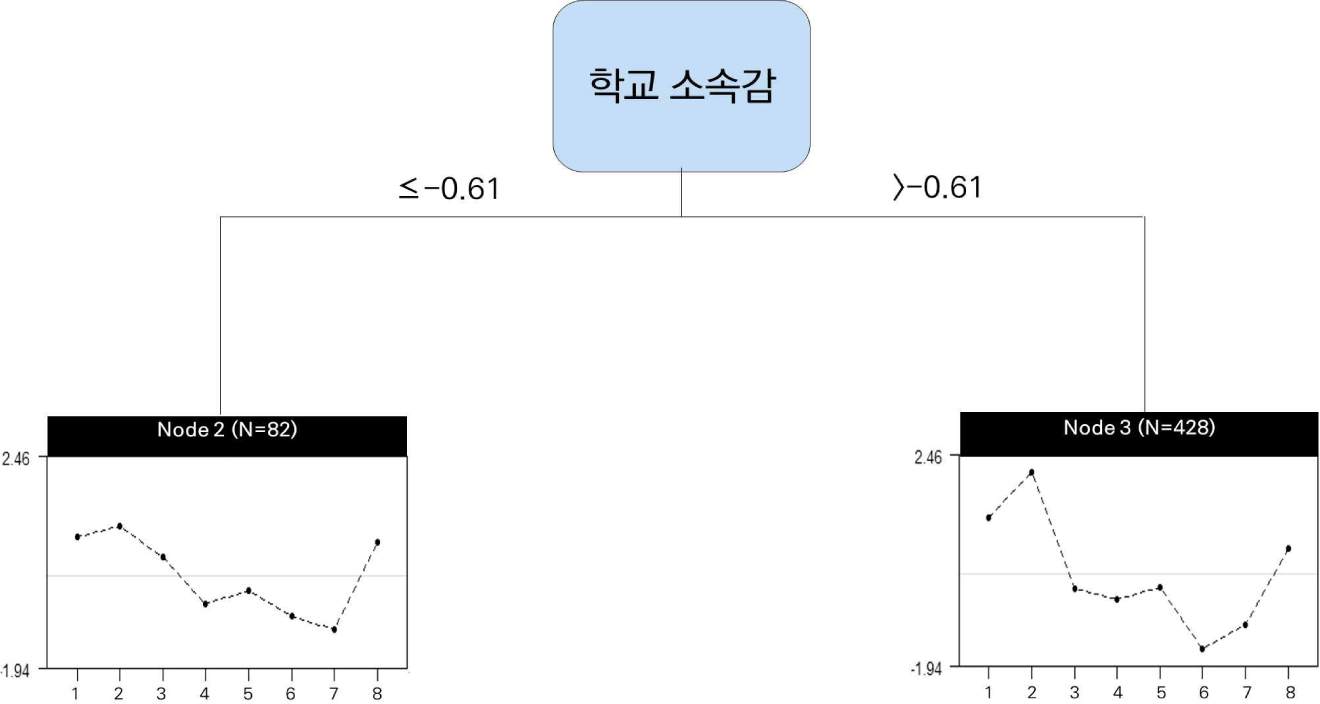
자료 A를 하위 집단별로 분할하여 추정된 문항 난이도를 분석한 결과, 8개 문항 중 1개 문항(Science Fair Poster – Q02)에서 하위 집단 간 난이도 차이가 기준치인 1 이상으로 나타나 차별기능문항에 해당하는 것으로 확인되었다. 참고로, ‘Science Fair Poster – Q02’ 문항은 시각적 표현에 해당하는 문항으로, 태양과 하나의 행성을 포함한 포스터를 제공한 후, ‘먼 우주에서의 생활’을 주제로 독창적인 방식으로 포스터를 발전시키는 문제 해결 과정을 측정하는 문항이다(OECD, 2024a). 해당 문항의 경우, ‘학교 소속감’이 자료 분할 기준점인 -0.61보다 높은 집단의 난이도(2.09)가 -0.61보다 낮거나 같은 집단의 난이도(1.02)에 비해 1.07만큼 높게 나타났다. 즉, ‘학교 소속감’이 -0.61보다 높은 집단은 -0.61보다 낮거나 같은 집단보다 해당 문항을 상대적으로 더 어렵게 느낀다는 것을 의미한다.
반면, 자료 B의 7개 문항의 차별기능문항 탐색 결과, 자료를 분할하는 변인이 없는 것으로 나타났다. 자료를 분할하는 변인이 나타나지 않았다는 것을 바탕으로 자료 B의 7개 문항에는 차별기능문항이 존재하지 않는다는 것을 알 수 있다. 자료 B에 해당하는 집단의 각 문항에 대해 추정된 난이도는 <표 4>와 같다.
다음, 자료 C의 7개 문항의 차별기능문항 탐색 결과를 나무구조로 표현하면 [그림 2]와 같다. 자료 C는 한 번의 자료 분할을 통해 2개의 하위집단이 도출되었다. 자료 분할은 창의적 사고력 관련 설명변인인 ‘창의성과 지적 개방성’에 의해 이루어졌으며 기준점은 -0.108로 나타났다. 하위집단별 각 문항에 대해 추정된 난이도는 <표 5>와 같다.
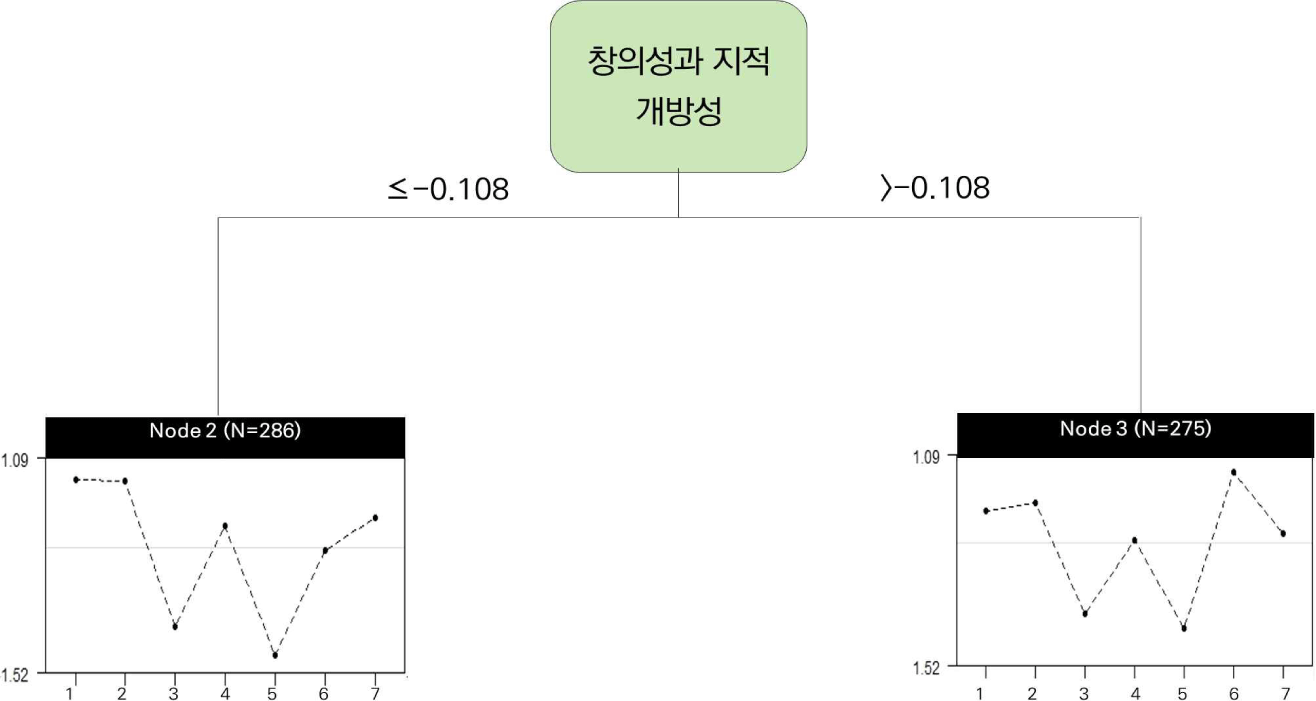
자료 C에서 ‘창의성과 지적 개방성’의 기준값 –0.108을 기준으로 높은 집단과 낮거나 같은 집단 간의 추정된 문항 난이도를 비교한 결과, 7개 문항에서는 난이도 차이가 1보다 큰 문항이 없어 차별기능문항이 존재하지 않는 것으로 나타났다.
마지막으로, 자료 D의 7개 문항의 차별기능문항 탐색 결과를 나무구조로 표현하면 [그림 3]과 같다. 자료 D는 두 번의 자료 분할을 통해 3개의 하위집단이 도출되었다. 첫 번째 자료 분할은 학생 개인 변인인 ‘성별(여학생=1, 남학생=2)’에 의해 분할되었으며, 두 번째 자료 분할은 수학역량 관련 변인인 ‘수학 학습에 대한 노력과 끈기’에 의해 이루어졌으며 기준점은 -0.477로 나타났다. 하위집단별 각 문항에 대해 추정된 난이도는 <표 6>과 같다.
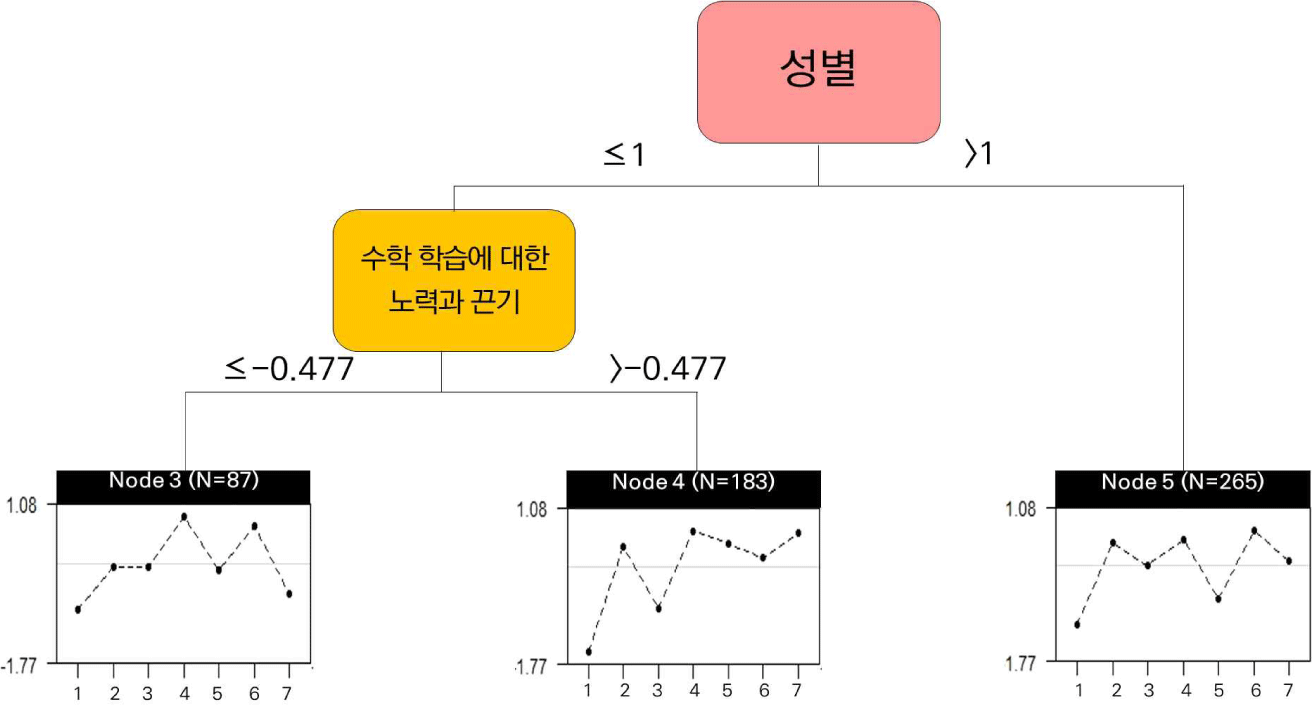
자료 D를 하위 집단별로 분할하여 추정된 문항 난이도 차이를 분석한 결과, 7개 문항 중 1개 문항(Rubber Duck Fishing GameQ01)에서 세 하위집단 간 난이도 차이를 비교한 결과, 두 개의 하위 집단간 난이도 차이가 1 이상으로 나타나 차별기능문항에 해당한다는 것으로 확인되었다. 구체적으로, ‘Rubber Duck Fishing GameQ01’ 문항의 경우, 여학생(성별=1)이면서 ‘수학 학습에 대한 노력과 끈기’가 -0.477보다 높은 집단의 난이도(0.43)가 남학생(성별=2) 집단의 난이도(-0.61)보다 1.04만큼 높게 나타났다. 이러한 결과는 여학생(성별=1) 중에서 ‘수학 학습에 대한 노력과 끈기’가 -0.477보다 높은 집단이 남학생 집단보다 해당 문항을 상대적으로 더 어렵게 느낀다는 것을 의미한다.
Rasch tree 분석은 자료 분할을 통해 도출된 하위집단의 문항 난이도에 대한 신뢰구간이 제공되지 않기 때문에 반복분석을 통해 원자료에 대한 Rasch tree 분석이 얼마나 안정적인지 확인할 필요가 있다. 본 연구에서는 분석에 활용된 원자료를 무선적으로 500번 재표집하고 이에 대해 반복분석을 실시하여 설명변인이 자료를 분할하는 변인으로 몇 번 추출되는지를 확인하였다. 각 자료에 대한 반복분석 결과는 <표 7>과 같다.
| 자료 A | |
|---|---|
| 변인명 | 횟수 |
| • 학교 소속감* | 33 |
| • ESCS | 15 |
| • 주말 여가 활동에서 ICT 활용 시간 | 7 |
| • 가정에서 보유한 도서 수 | 2 |
| • 수학에 대한 쉬움 인식 • 수학 자기효능감: 추론과 21세기 수학 • 학교 밖에서의 ICT 접근성 • 디지털 기기 사용 시간 • 부모의 창의성과 지적 개방성 |
1 |
| 계 | 62 |
| 자료 B | |
|---|---|
| 변인명 | 횟수 |
| • 가정에서 보유한 도서 수 | 23 |
| • 학교 활동 참여도 | 7 |
| • 학습 지속을 위한 학교의 지원 활동 | 6 |
| • 학생이 기대하는 직업 지위 • 인내심 • 수학 개념 친숙도 • ICT를 활용한 수학 활동 |
3 |
| • 학교 소속감 | 2 |
| • 성별 • 학생-교사관계의 질 • ESCS • 학교에서의 ICT 접근성 • 학교 밖에서의 ICT 사용(학교 활동) |
1 |
| 계 | 55 |
먼저, 자료 A를 500번 재표집하여 반복 분석한 결과, 원 자료에서 자료를 분할하는 설명변인으로 나타난 ‘학교 소속감’이 500번의 반복 분석에서도 33회로 가장 많이 자료를 분할하는 설명변인으로 확인되었다. 다음으로 ‘ESCS’이 15회로 나타났으며, ‘주말 여가 활동에서의 ICT 활용 시간’이 7회, ‘가정에서 보유한 도서 수’가 2회 자료를 분할하는 변인으로 확인되었다. 이외에도 ‘수학에 대한 쉬움 인식’, ‘수학 자기효능감: 추론과 21세기 수학’, ‘학교 밖에서의 ICT 접근성’, ‘디지털 기기 사용 시간’, ‘부모의 창의성과 지적 개방성’이 각각 1회씩 자료를 분할하는 설명변인으로 도출되었다, 자료 A에서 차별기능을 유발하는 변인이 도출된 총 횟수는 62회였다. 한편 자료 B에 대한 반복분석 결과, ‘가정에서 보유한 도서 수’가 23회로 가장 많이 자료를 분할하는 변인으로 확인되었으며, ‘학교 활동 참여도’, ‘학습 지속을 위한 학교의 지원 활동’이 각각 7회, 6회로 나타났다. 이외의 변인은 5회 미만으로 도출되었다. 차별기능을 유발하는 변인이 도출된 총횟수는 55회였다.
또한, 자료 C에 대한 반복분석 결과, 원 자료에서 자료를 분할하는 것으로 나타난 ‘창의성과 지적 개방성’이 82회로 가장 많이 자료를 분할하는 변수로 도출되었다. 그 다음으로 ‘(교내) 창의적 활동 참여’가 60회, ‘형식적/응용 수학 과제 노출’이 27회, ‘성별’이 19회 순으로 많이 도출되었다. 이외의 변인은 5회 미만으로 나타났으며, 차별기능을 유발 변인이 도출된 횟수는 총 206회로 나타났다.
마지막으로, 자료 D에 대한 반복분석 결과, 원 자료에서 자료를 분할하는 변인으로 나타난 ‘성별’이 50회로 가장 많이 자료를 분할하는 것으로 확인되었으며, ‘수학 학습에 대한 노력과 끈기’도 11회 자료를 분할하는 변인으로 도출되었다. 이외에도 ‘가정에서 보유한 도서 수’가 37회, ‘수학 자기효능감: 추론과 21세기 수학’이 9회, ‘자기주도학습에 대한 효능감’아 6회 순으로 자료를 분할하는 변인으로 도출되었다. 이외의 변인은 5회 미만으로 나타났다. 차별기능 유발 변인 도출 횟수는 총 137회로 확인되었다.
한편, Rasch tree 분석 결과에 대한 안정성 평가를 실시한 선행연구(고수경 외, 2024; 장윤선, 이주연, 2023; Philipp, Zeileis & Strobl, 2016)에서는 자료를 분할하는 변인으로 도출된 횟수가 50% 이상일 경우 이를 차별기능문항 유발에 안정적인 변인으로 간주하고 있다. 본 연구에서 원 자료에서 자료를 분할하는 것으로 도출된 설명변인의 500번 반복분석에서의 도출비율을 살펴보면, 원 자료 A의 ‘학교 소속감(6.6%)’, 자료 C의 ‘창의성과 지적 개방성(16.4%)’, 자료 D의 ‘성별(10%)’, ‘수학 학습에 대한 노력과 끈기(2.2%)’로 나타나, 차별기능문항을 안정적으로 유발하는 변인으로 간주하기에는 기준치인 50% 이상을 충족하지 못했다. 이는 분석 자료나 설명변인의 조합에 따라 도출된 집단 간 차별 기능에 미치는 영향이 일관되지 않음을 의미한다고 볼 수 있다. 이러한 기준을 고려하였을 때, PISA 2022 창의적 사고력 영역에서는 차별기능문항을 일관적으로 유발하는 변인이 없어 차별기능문항이 존재하지 않는 것으로 해석할 수 있다.
V. 결론 및 제언
본 연구는 PISA 2022 창의적 사고력 영역에 Rasch tree 방법을 적용하여 다양한 설명변인을 바탕으로 차별기능문항을 탐색하고 이를 유발하는 변인을 확인하였다. 또한 이에 대한 안정성 평가를 통해 차별기능문항을 유발하는 설명변인이 차별기능에 미치는 영향이 일관적인지 확인하였다. 주요 결과를 바탕으로 한 시사점은 다음과 같다.
PISA 2022 창의적 사고력 측정 문항에 대한 차별기능문항을 탐색한 결과, 총 31개 문항 중 2개의 문항이 분석 자료의 조합에 따라 학교 관련 변인인 ‘학교 소속감’, 창의적 사고력 관련 변인인 ‘창의성과 지적 개방성’, 학생 개인 관련 변인인 ‘성별’, 수학 역량 관련 변인인 ‘수학 학습에 대한 노력과 끈기’의 설명변인에 의해 도출된 하위집단 간 난이도 차이가 기준치를 초과하여 차별기능이 유발되는 것으로 확인되었다. 다만 이에 대한 안정성 평가를 위해, 500번의 재표집을 통해 반복 분석을 실시한 결과 4개 설명변인 모두, 분석 자료의 조합에 따라 차별기능에 미치는 영향이 일관되지 않게 나타났다. 이러한 결과는 창의적 사고력 영역의 31문항 중 차별기능문항이 존재하지 않음을 의미한다. PISA 2022 창의적 사고력 영역에서 차별기능문항이 나타나지 않았다는 것은 다양한 설명변인에 의한 편파가 나타나지 않는다는 것을 의미한다는 점에서 검사의 공정성 측면에서 유의미한 결과라고 볼 수 있다. 이러한 결과는 Rasch tree 방법을 적용하여 단순히 범주형 변인을 활용하거나 연속형 변인을 특정 기준값으로 구분하여 사전에 집단을 구분해야 하는 전통적인 방법의 한계를 벗어나, 자료에 포함된 다양한 설명변인을 활용해 차별기능문항을 탐색하였다는 데 의의가 있다.
Rasch tree 방법을 적용하여 차별기능문항을 탐색한 결과, ‘학교 소속감’, ‘창의성과 지적 개방성’, ‘성별’, ‘수학 학습에 대한 노력과 끈기’에 의해 자료가 분할되어 하위집단에 따라 문항 난이도의 차이가 나타났다. 이는 하나의 변인에 의해 차별기능문항이 유발되는 것이 아닌 다양한 설명변인의 상호작용에 의해 차별기능문항이 유발된다는 것을 의미한다고 볼 수 있다. PISA 2022에서 창의적 사고력은 학생들이 일상에서 보여줄 수 있는 창의적 사고 유형을 반영하였기 때문에(OECD, 2023) 기존의 차별기능문항을 탐색하는 선행연구에서 활용한 성별이나 국가 등 단순한 변인뿐만 아니라 다양한 변인의 차이로 인한 차별기능문항이 발생할 수 있다. 이는 하나의 변인으로 사전에 집단을 구분하여 차별기능문항을 탐색하는 전통적인 방법으로는 차별기능문항을 충분히 탐색할 수 없다는 것을 의미한다. 따라서 차별기능문항을 탐색하는데 다양한 설명변인을 적용하여 다양한 변인의 상호작용에 의해 나타날 수 있는 차별기능문항을 확인할 필요가 있다. 본 연구에서 활용한 PISA 자료뿐만 아니라 국내외에서 시행되고 있는 학업성취도 평가에서는 학생들의 성취도를 측정할 뿐만 아니라 학생, 교사, 학부모, 학교 등 다양한 대상에게 설문조사를 실시하여 교육맥락변인을 파악하고 있다. 대규모 자료를 제공할 뿐만 아니라 이에 대한 다양한 분석을 시행하여 실증적 데이터에 기반한 교육정책을 개발하고 추진하는데 목적을 두고 있다. 데이터에 기반하여 실제 도움이 되는 교육정책을 개발하기 위해 검사의 공정성에 영향을 미칠 수 있는 차별기능문항을 탐색하는 것은 매우 중요한 과정이라고 볼 수 있다. 이때 단순히 하나의 변인을 사전에 선정하여 차별기능문항을 탐색하는 것이 아닌 자료에 포함된 다양한 교육맥락변인을 바탕으로 데이터 기반의 차별기능문항을 탐색해야 할 필요가 있다. 이를 통해 실증적 데이터에 기반하여 학생들에게 실제적으로 도움이 될 수 있는 정책을 개발하고 추진해야 할 것이다.
Rasch tree 방법은 문항반응이론의 Rasch 모형에 기반하여 하위집단별 난이도를 추정하여 난이도 차이를 바탕으로 차별기능문항을 확인하는 방법이다. 하지만 하위집단별로 추정된 난이도에 대해 신뢰구간을 제공하지 않아 통계적으로 유의한 수준의 난이도에 차이가 존재하는지 확인하기 어렵다는 한계점을 가진다. 이에 본 연구에서는 난이도 차이가 1보다 큰 경우 차별기능문항으로 정의하였으며, Rasch tree 방법을 적용하여 차별기능문항을 탐색한 선행연구(장윤선, 이주연, 2023)에서도 추정된 난이도의 범위에 따라 연구자가 임의로 기준값을 정하여 하위집단별 난이도 차이가 기준값보다 크면 해당 문항을 차별기능문항으로 보았다. 이러한 한계점을 보완하기 위해 Rasch tree 방법은 자료에 대한 재표집과 반복분석을 통해 안정성 평가를 실시하여 차별기능문항과 이를 유발하는 변인이 차별기능에 미치는 영향이 일관적인지 확인하는 과정이 필요하다. 이러한 점은 Rasch tree 방법을 차별기능문항을 탐색하는데 있어 탐색적 연구로 활용할 수 있음을 시사한다. 먼저 Rasch tree 방법을 통해 차별기능문항을 유발하는 변인과 그 기준점을 확인한 후에 해당 변인과 기준점을 활용하여 통계적 유의성을 검증이 가능한 차별기능문항 탐색 방법을 활용할 수 있을 것이다. 즉, 차별기능문항을 도출하는데 Rasch tree 방법을 탐색적 접근으로 활용하고 결과에 대해 확인적 접근을 통해 확인한다면 자료에 포함된 다양한 설명변수를 활용함과 동시에 통계적인 유의성을 확인하여 차별기능문항을 탐색할 수 있을 것이다.
본 연구는 PISA 2022 창의적 사고력 영역의 차별기능문항을 탐색하는데 있어 집단을 사전에 정의하는 전통적인 방법에서 벗어나 기계학습 기반의 재귀적 자료 분할 기법을 적용하여 다양한 설명변인을 바탕으로 차별기능문항을 탐색하고 이를 유발하는 변인이 미치는 영향이 일관적인지 확인하였다는 데 의의가 있다. 이를 통해 PISA 2022 창의적 사고력 영역에 차별기능문항이 존재하지 않음을 밝히고, 평가 결과를 바탕으로 학생들의 창의적 사고력을 향상시킬 수 있는 방안을 마련해야 할 필요가 있다는 점에서 후속연구의 필요성을 확인할 수 있었다. 또한 최근 성취도뿐만 아니라 교육맥락변인을 함께 조사한다는 점에서 다양한 설명변인을 포함하는 대규모 자료를 분석하고 활용하는 것이 중요해지고 있기 때문에 자료에 포함된 다양한 설명변인을 활용하여 차별기능문항을 탐색하였다는 점에서 의의가 있다. 본 연구에서는 Rasch tree 적용을 위해 부분점수가 포함된 문항을 이분형 문항으로 변환하여 활용하였지만, 최근 대규모 표준화 검사에서는 구성형 문항을 포함하여 부분점수를 활용하고 있으며, 학생들의 특성을 파악하기 위한 설문조사에서는 대부분 4, 5점 척도로 측정하고 있다. 따라서 이러한 자료를 변환 없이 활용하기 위해 다분문항에 나무구조를 적용하여 차별기능문항을 탐색하는 방법에 대한 연구가 이루어지길 기대한다. 본 연구에서 활용된 Rasch tree 방법은 데이터를 기반으로 차별기능문항을 탐색하는 방법으로 한국 학생들의 PISA 2022 창의적 사고력 자료에 한정된 결과라고 볼 수 있다. 따라서 보다 더 다양한 데이터를 활용하여 분석한 연구결과를 추후 연구를 통해 확인할 필요가 있을 것이다. 또한 차별기능문항을 탐색할 때, 두 가지 이상의 방법을 활용하는 것이 효과적이라는 점(Lai, Teresi, & Gershon, 2005)에서 차별기능문항을 탐색하는 다른 방법을 함께 적용하여 비교할 필요가 있을 것이다. 이를 통해 창의적 사고력에 대한 공정한 검사가 시행되고, 이에 대한 결과를 바탕으로 학생들의 창의적 사고력을 향상시킬 수 있는 방안을 마련해야 할 것이다.







