I. 서 론
학습 결과에 대한 평가라는 기존 패러다임으로부터 학습자의 개별적인 학습과 성장을 촉진하기 위한 방향으로 평가의 패러다임이 변화함에 따라(Campbell, 2012), 구성형 문항 또는 개방형 문항을 활용한 평가가 중요해지고 있다. 선다형 문항과 비교하여 개방형 문항의 답안에서는 학습자의 사고 및 추론 과정이 답안에 더 잘 드러나기에(Santos & Cai, 2016), 학습자의 구체적인 문제해결 과정이나 개념 이해 수준을 쉽게 관찰하고 적합한 피드백을 제공할 수 있다(박세진, 하민수, 2020). 그러나 이러한 서술식 답안의 채점에는 선다형 문항과 비교했을 때 훨씬 많은 시간과 자원이 필요하고, 채점의 일관성과 신뢰도를 유지하기 쉽지 않다.
이러한 맥락에서 인공지능의 발전에 따라 자동 채점 기술이 평가에 관해서도 새로운 지평을 열어주고 있다. 자동 채점은 자연어로 작성된 답안을 읽고 처리하며 채점하는 지능적 행위를 인공지능이 수행하는 것(이경건, 하민수, 2020)으로, 컴퓨터를 이용하여 영어 에세이를 채점하려는 Page(1966)의 연구가 그 시초라 할 수 있다. 자동 채점은 인공지능의 발전에 따라 기초적인 기계학습부터 딥러닝, 최근 트랜스포머 기반의 대규모 언어모델에까지 그 기술적 기반을 확장해 가고 있다. 교육 현장에서의 자동 채점 사용에 대한 우려와 부정적 견해도 있으나, 즉각적인 피드백을 통해 학습 효과를 유의미하게 증진할 수 있다는 점(Zhu et al., 2017)이나 학습자 중심의 맞춤형 수업 구현, 교사의 업무부담 감소(이경건, 하민수, 2020) 등 자동 채점의 여러 장점이 있으므로 관련 연구가 지속될 필요가 있다.
자동 채점은 이미 학문적 탐구 영역에서 실제 활용의 영역으로 전환되고 있다(Williamson et al., 2012). 특히 언어나 과학 교과에서는 타 교과와 비교하여 자동 채점 연구가 비교적 많이 진행되었는데, 먼저 언어 교과에서는 Page(1966, 1994)의 연구를 기초로 개발된 PEG(Project Essay Grade)나 미국교육평가원(Educational Testing Service: ETS)의 e-rater(Burstein et al., 1998) 등이 이미 인간 채점 결과의 확인 평가자로서 상업적으로 활용되고 있다(김승주, 2019). 과학 교과에서도 상업 목적으로 시행되는 ETS의 c-rater를 사용한 중학교 과학 문항 평가가 이미 인간 채점자 수준의 신뢰도를 보였다(Liu et al., 2014; Liu et al., 2016). 국내에도 작문 및 영어, 과학 교과 자동 채점 연구가 진행되고 있다(이상하 외, 2015; 조희련 외, 2021; 이용상, 박강윤, 2022; 박강윤 외, 2021; 박세진, 하민수, 2020). 이와 달리 수학 교과의 구성형 답안 자동 채점의 경우 국외의 최근 연구는 뒤에 제시할 바와 같이 몇 개의 문항에 자동 채점 모델을 적용한 학문적 탐구 또는 가능성을 확인하는 수준의 연구들이 대부분이고, 국내에서도 비교적 최근에서야 이루어지고 있다(최인용 외, 2024; 신병철 외, 2024). 그러나 수학 교과는 오랫동안 K-12 교육과정의 기본이자 필수적인 과목으로 여겨져 온 만큼(McConney & Perry, 2010), 수학 교과에서도 자동 채점을 통한 학생평가의 개선이 시급한 과제라 할 수 있다.
본 연구는 수학 교과 구성형 문항 답안의 자동 채점 연구들을 분석하여 전반적인 선행 연구의 동향을 살피고, 그 결과로부터 논의할 점과 향후 연구의 방향성을 도출하고자 하였다. 학습자가 다양하게 답안을 제시할 수 있는 문항을 설명하기 위해 선행 연구가 사용한 용어로는 학습자가 직접 구성한 답안을 의미하는 ‘구성형 답안(constructed-response)’(Livingston, 2009), 열려 있는 답안을 뜻하는 ‘개방형(open-ended)’(Becker & Shimada, 1997; Hertzog, 1998) 등이 있었다. 반면, 국내에서 비슷한 의미로 사용되는 서술형(descriptive) 평가는 목표 행동 및 사건에 대한 전후 관계를 기록하는 방식의 평가(Anderson et al., 2006)를 의미한다. 관련 선행 연구를 살펴본 결과 용어 간 의미가 혼용되는 경우가 많았기에 본 연구에서는 선행 연구의 내용을 확인하거나 인용하는 부분에서는 될 수 있으면 원문의 표현을 그대로 사용하였고, 그 외에는 이 중에서 연구의 목적과 가장 가까운 의미의 용어인 ‘구성형’으로 용어를 통일하여 사용하였다.
본 연구는 수학 교과에서의 구성형 자동 채점 관련 선행 연구를 살펴보기 위해 체계적 문헌 고찰의 방법을 사용하였다. 특히 본 연구는 구성형 답안의 형태에 따른 분류기준을 제안하고 이에 따라 선행 연구를 분석하였다.
본 연구에서 설정한 연구 문제는 다음과 같다.
첫째, 수학 교과의 구성형 답안 자동 채점 연구는 어떤 학교급 및 주제 영역에서 주로 이루어지고 있는가?
둘째, 수학 교과의 구성형 답안 자동 채점 연구에서는 어떤 데이터와 알고리즘 및 채점 방법을 사용하여 어떤 성능을 보였는가?
셋째, 기존 연구를 답안의 형태 및 입력 유형에 따라 구분한 결과는 어떠한가?
II. 이론적 배경
초기 인공지능 기반 자동 채점 연구는 영어 에세이를 컴퓨터로 자동 채점하려는 Page(1966)의 규칙 기반 자동 채점 연구로부터 시작되었다. 그는 채점에 필요한 중요한 자질(feature)을 추출하여, 답안의 채점 자질과 그 답안에 대한 전문가의 채점 점수 간의 관계를 통해 답안에 대한 점수를 예측하는 방식의 자동 채점 모델을 개발하였다. 채점 모델의 성능을 평가하기 위해 피어슨 상관계수 또는 이차 가중 카파(Fleiss & Cohen, 1973)를 사용하는 방법이 초기부터 확립되었고, 후술할 자동 채점도 이를 일반적인 평가 지표로 사용한다. 규칙 기반의 자동 채점 연구사례로는 PEG, e-rater 등이 있다(박종임 외, 2022).
기계학습은 데이터로부터 기계가 지식을 스스로 습득하는 귀납적 방법으로, 대량의 데이터를 저장하고 처리할 수 있는 환경이 마련되면서 기계학습 연구가 본격적으로 시작되었다. 분류나 회귀, 추론 등 통계 처리를 기반으로 한 기계학습이 가능해지면서 자동 채점 기술도 다양한 방식으로 발전하였다. 예컨대 자연어처리 기술이 적용된 ETS의 c-rater는 답안이 수학, 과학 개념을 잘 표현하는지를 문장 단위로 식별하는 자동 채점 엔진으로, 인간 채점자와의 일치율이 평균 84%에 달하는 성능을 보였다(Leacock & Chodorow, 2003; Liu et al., 2014). 또한 PISA 2012 결과를 분석한 연구들(Saarela et al., 2016; Pejić et al., 2021)은 다양한 기계학습 알고리즘을 적용하여 대규모 평가에서 학생의 수학적 능력을 예측하였다. Zhai 외(2020)의 문헌 연구는 일반적인 기계학습 유형의 분류를 과학 교과 자동 채점에 적용하여 지도학습과 비지도학습, 준지도학습으로 분류하였다. 채점의 정확성을 위해 지도학습 방법이 자동 채점에서 보편적으로 사용되었으나, 기술의 발전 및 연구 진척에 따라 다양한 기계학습 알고리즘이 적용되고 있다.
자동 채점 연구는 딥러닝 알고리즘의 도입과 함께 발달한 여러 인공지능 모델을 통해 다양하게 확장되고 있다. 인공신경망(Artificial Neural Network)이란 인간의 두뇌를 모방하여 인공 뉴런이 상호 결합하는 구조를 구성하도록 설계된 모델(van Gerven, 2017)이다. 비교적 단순한 구조로 시작된 인공신경망은 모델 내 은닉층을 늘리는 딥러닝 방식이 도입되면서 획기적인 성능 개선을 이루었고, 이를 응용하는 많은 알고리즘이 개발되었다. 특히 자연어처리에 주로 사용되는 순환신경망(Recurrent Neural Network)이나 이미지처리에 좋은 성능을 보이는 합성곱 신경망(Convolution Neural Network; CNN) 등이 학습자의 구성형 답안을 자동 채점하는 딥러닝 모델로써 주로 활용되고 있다. 특히 자동 채점 분야에서도 숫자나 보기를 손글씨로 작성한 답안을 인식하는 연구들(Brown, 2017; Shaikh et al., 2019; 이재봉, 2023)이 이루어졌다.
최근 트랜스포머 기반의 GPT(Generative Pre-trained Transformer), BERT(Bidirectional Encoder Representations from Transformers) 등의 언어모델을 이용한 자동 채점 연구도 이루어지고 있다. 트랜스포머(transformer)란 셀프 어텐션(self-attention) 기법을 이용한 신경망 구조로, 기존 순환신경망이나 합성곱 신경망보다 우수한 성능을 내는 모델이다(Vaswani et al., 2017). OpenAI의 언어 생성 모델 GPT(Radford et al., 2018)나 구글의 자연어처리 모델 BERT(Devlin et al., 2019)가 모두 이를 기본으로 한다. 먼저 GPT는 자연어처리를 위해 트랜스포머의 디코더를 다층적으로 쌓은 구조의 모델로, 주어진 단어들을 바탕으로 문맥에 따라 다음 단어를 예측하는 방식으로 작동하여 문장 생성에 강점을 보인다. 프로그래밍, 작문, 수학 등 여러 영역에서 이를 활용하여 학습 피드백을 제공하는 연구가 이어지고 있다(Pankiewicz & Baker, 2023; Dai et al., 2023; Carlson et al., 2023; Rane, 2023; Bernal, 2024). 이에 반해 BERT는 트랜스포머의 인코더를 다층 쌓은 구조로, 대용량의 사전 학습 데이터를 이용하여 언어모델을 구축한 뒤 특정 작업을 위한 신경망을 추가한 전이학습 모델이다. 기본적인 BERT 모델을 파인 튜닝(fine-tuning)한 모델 중 Sentence-BERT는 코사인 유사도로 의미론적으로 유사한 문장을 찾거나 군집화하는 작업의 효율을 높인 모델로(Reimers & Gurevych, 2019), 이를 사용하여 자동 채점하는 여러 연구가 이루어지고 있다(Beseiso & Alzahrani, 2020; Fernandez et al., 2022; Baral et al., 2023) GPT나 BERT 기반의 대규모 언어모델 역시 자동 채점을 위해 사용되고 있다. 대규모 언어모델은 적절한 파인 튜닝을 거쳐 기본 모델보다 특정 작업에서 더 높은 성능을 보이는데, 다중 클래스로 답안을 채점한 연구(Latif & Zhai, 2024)나 확산적 사고를 측정한 연구(Organisciak et al., 2023)에서 파인 튜닝의 효과성이 보고되었다.
Popham(1997)은 평가 기준의 필수 요소로 평가 항목, 질적 정의, 채점 전략을 제시하였는데, 채점 전략을 답안 전체에 총점을 배정하는 총체적 채점법(holistic scoring)과 각각의 세부적인 평가 항목에 대해 부여한 점수의 총합을 총점으로 하는 분석적 채점법(analytic scoring)으로 구분하였다. 먼저, 총체적 채점법은 학습자의 답안에서 개념이나 절차적 이해, 수학적 의사소통 및 추론, 문제해결 등을 평가하는 루브릭을 사용한다. 이 방법은 채점에 적은 시간이 필요하지만, 평가자 간의 일치도가 낮을 수 있다는 단점이 있다(Taylor, 1998). 대부분의 수학적 글쓰기의 채점 과정은 답안에서 나타나는 인지적 이해 수준을 식별하는 데에 중점을 둔다(Powell et al., 2017). 예컨대 Evens & Houssart(2004)는 학생의 답안을 표현 능력과 추론 능력에 따라 미작성, 오류 및 무관한 답변, 재진술, 예시 제시, 정당화 등으로 분류하였고, Baxter 외(2005)도 학생의 이해 수준에 따라 기록 단계부터 요약, 일반화, 연관 짓기로 답안을 분석하였다. 본 연구는 총체적 채점법을 좀 더 일반적으로 구분하여 정답 여부만 식별하는 이분형(binomial)과 특정 점수나 수준에 따라 여러 단계로 구분하는 다분형(multinomial)의 방식으로 나누었다.
이와 달리 분석적 채점법은 기준요소별로 점수를 할당하여 채점한 뒤 이를 합산하는 방식으로, 기준요소를 정하는 과정은 복잡하지만, 평가자 간의 일치도를 좀 더 확보할 수 있다. 수학적 내용 지식이나 개념, 수학적 절차, 작문의 특정 요소 등 여러 요소를 기준요소로 정할 수 있는데, Namkung 외(2020)는 사칙연산을 사용하는 다단계 문제에 대하여 수학적 내용과 수학 어휘, 작문 구성과 작문 문법이라는 네 개의 기준요소를 설정하였다. 다만 본 연구에서 분석한 바와 같이 수학 교과의 구성형 답안 채점에서는 타 교과에서 보편적으로 사용되는 기준요소별 분석적 채점법보다는, 수식이나 수학적 논리의 전개에 따른 단계별 분석적 채점법이 주로 사용된다는 특수성이 있다. 예컨대, 과학 교과에서는 답안에 핵심 개념어의 포함 여부를 독립적으로 확인하는 방식의 채점이 가능하다(Lee et al., 2023). 그러나 수학 교과의 답안은 문제 접근 방법에 따라 풀이 방법이 다양하기도 하고, 개념적 지식을 알더라도 수학적 모델링 과정이나 풀이, 계산 과정에서 오류 및 실수가 생기기도 한다(Noutsara et al., 2021). 즉, 채점 요소에 따른 분석적 채점법을 적용할 때, 독립적인 채점 요소로 구분하는 방식 외에 논리 전개 과정에 따라 채점 요소를 구분하는 방법이 필요한 경우가 많다. 본 연구는 이에 주목하여 분석적 채점법을 병렬적 요소별로 채점한 방식과 답안의 흐름 순서에 따라 채점한 방식으로 구분하였다. 특히 답안에서 서로 독립적 혹은 병렬적 요소별로 채점하는 방법을 요소형 분석적 채점법(elements analytic scoring)으로, 풀이 과정에서 드러난 논리 전개 과정 단계에 따라 점수를 부여한 단계형 분석적 채점법(step-by-step analytic scoring)으로 각각 구분하여 명명하고 분석하였다. 이를 종합한 것은 다음 <표 1>과 같다.
총체적 채점법과 분석적 채점법은 자동 채점에서도 마찬가지로 적용될 수 있다. 예컨대 Jescovitch 외(2021)는 학부 생리학 과목 문항을 자동 채점하는 연구에서 이 두 채점법의 성능을 비교하였는데, 기계학습 채점 모델과 인간 채점자와의 일치도가 총체적 채점법은 0.75에서 0.87, 분석적 채점법은 0.78에서 0.89의 카파 계수를 보이는 등 두 채점법 모두 상당한 수준에서 인간 채점자의 것과 합치하는 결과를 얻었음을 보고하였다.
앞에서 본 것처럼 자동 채점 연구는 답안의 형태에 따라 자연어처리나 이미지처리 등 적절한 인공지능 모델을 사용하는 방식으로 이루어져 왔다. 답안의 형태에 따라 자연어처리나 이미지처리 등 적절한 인공지능 모델을 사용하여 자동 채점을 한다는 것은 답안의 형태에 따라 자동 채점 연구도 범주화할 수 있음을 의미한다. 김래영 외(2012)는 오하이오주의 학업성취도 평가를 분석하는 연구에서 학습자의 사고능력과 표현을 더 폭넓게 평가하기 위해 학습자가 수식이나 그래프, 다른 수학적 도식 표현 등 다양한 방식으로 답안의 근거 및 설명을 작성할 수 있도록 해야 한다고 주장하였다. 이처럼 수학 교과의 구성형 답안은 문장뿐만 아니라 수식, 그래프, 수학적 도식 등 여러 형태로 나타난다는 특수성이 있다. 따라서 인공지능 기술을 이용해 수학 구성형 답안을 자동 채점할 때에도 다양한 형태의 답안을 채점하는 것이 요구된다.
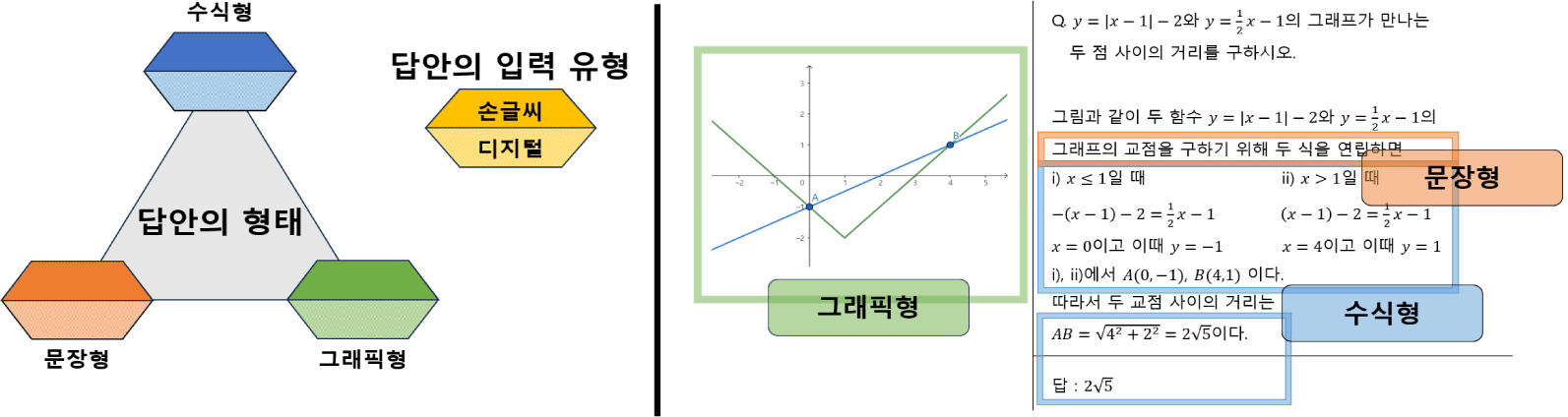
수학 답안의 형태를 구분한 선행 연구에 따르면 복잡한 수학 답안은 답안의 형태에 따라 수치 답안, 방정식, 그래프로 구분할 수 있다(Fife, 2017). 그러나 이 연구는 이미지 또는 자연어 형태의 답안이나 표현 양식이 혼합된 형태의 답안, 컴퓨터로 입력된 답안과 손글씨 답안을 구분하지 않았다는 한계점이 있다. 이에 본 연구는 위 견해를 자동 채점의 구현 원리에 맞게 개선하여 답안의 형태에 따른 분류기준을 문장형(sentence type), 수식형(mathematical formula type), 그래픽형(graphic type)으로 구분하였다. 이에 더하여 컴퓨터 환경에서 수집된 답안과 손글씨로 작성된 답안의 차이를 식별하고자 답안의 입력 유형도 포함하였다([그림 1] 참고). 물론 실제 평가 문항의 답안은 제시한 기준에 따라 완전히 상호 배타적인 것은 아니므로, 답안에서 위 기준에 해당하는 요소가 중복하여 식별될 수 있다.
먼저, 문장형 답안은 일반적인 자동 채점에서와같이 문장 형태로 서술된 답안을 의미한다. 수학 교과에서는 어떤 수학적 개념이나 상황을 글로 설명하는 형태라 할 수 있으며, 수학적 용어의 정확한 사용, 설명의 타당성 등이 채점의 주요 요소가 된다. 답안의 입력 형태의 관점에서 보았을 때 손글씨 답안은 문자 인식 과정을 통해 디지털로 변환되어 자동 채점의 대상이 되며, 디지털 형태의 답안은 추가적인 변환 과정 없이 입력받은 문자열 그대로 자동 채점된다.
다음으로 수식형 답안은 문항의 답을 도출하기 위해 수식 풀이 과정이 전개되고, 그 과정이 수학적으로 논리적이고 정확한지가 주목되는 답안을 뜻한다. 최병홍 외(2023)는 수학 서술형 문항은 그 풀이가 논리적 연결성이 요구되는 여러 명제의 나열로 이루어지는 경우가 많다고 하였다. 수학적 명제에는 문장 외에도 다양한 수식이 포함된다는 점에서 볼 때, 수학 구성형 답안에서는 타 교과의 답안과 달리 답안에 등장하는 수식이 채점 요소가 되는 경우가 많다. 따라서 수식을 제대로 이해하고, 논리적 연결성과 수식의 동등성, 오류를 판단하는 것이 중요하다.
마지막으로 그래픽형 답안은 기하학적 대상을 포함한 수학적 대상을 그림 또는 그래프로 그린 답안이다. 수학 교과의 구성형 문항 중에는 그림 또는 그래프로 답하는 경우가 있는데, 도형을 이용한 기하학적 표현은 기초적인 수학 학습 과정부터 중요하게 다루어지며, 방정식의 해를 구하기 위해 그래프가 이용되기도 한다. 이를 채점하려면 그래픽 형태로 표현된 답안 중 기하학적으로 중요한 특징이나, 문항이 요구하는 핵심 부분이 잘 표현됐는가에 주목해야 한다. 이와 관련하여 Fife(2013)는 채점 모델이 그래픽 답안을 인식할 때 약간의 오차를 허용하도록 함으로써 개념의 이해 및 과제 수행 능력과 상관없이 발생하는 채점 오류를 줄이는 방법을 제안하였다. 이처럼 추상적인 대상을 다루기 위해 다양한 도식을 이용할 수 있는데, 자동 채점 모델이 답안으로부터 필요한 요소에 주목하여 채점할 수 있도록 하는 것이 중요하다.
III. 연구 방법
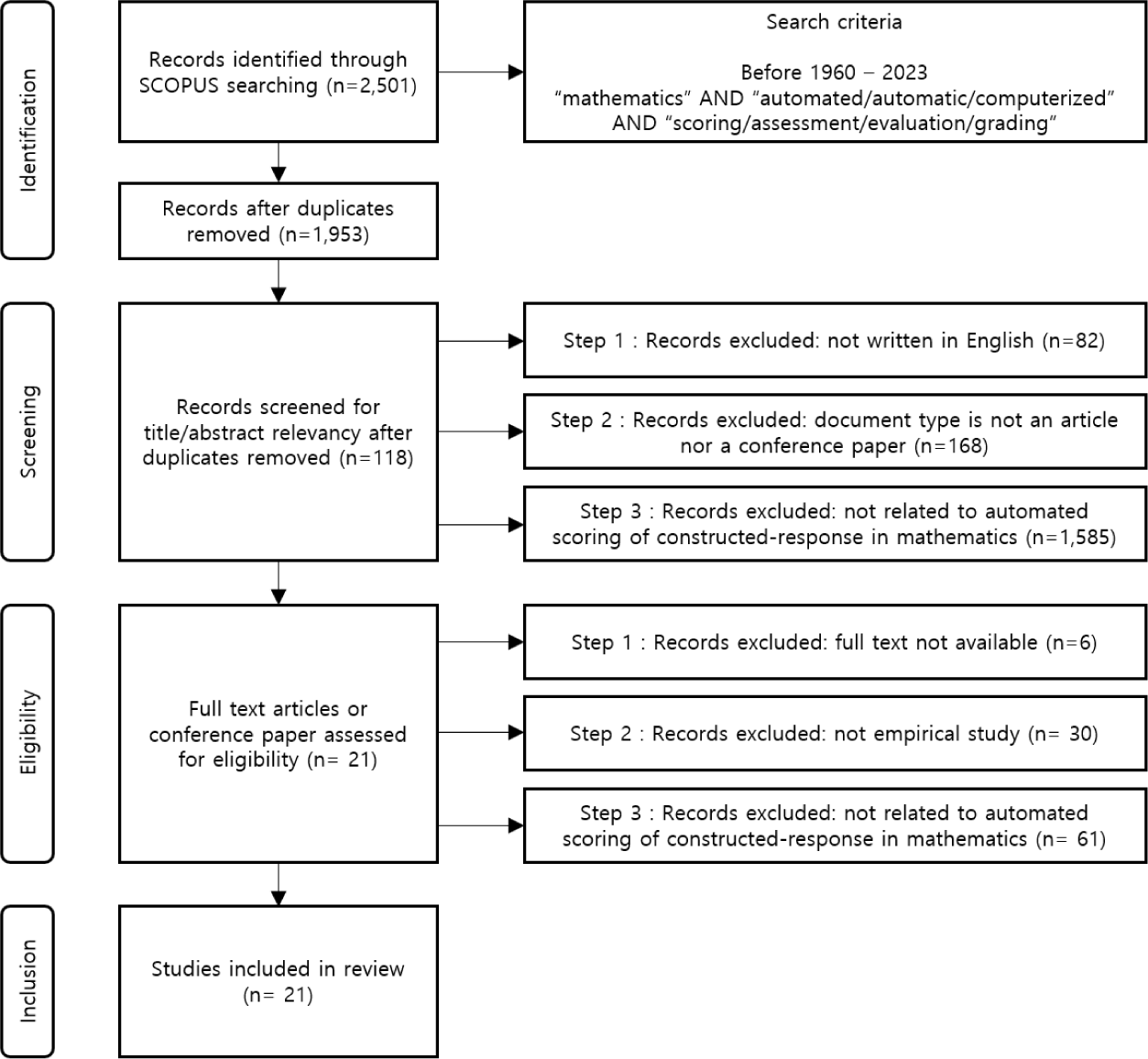
본 연구는 국제 학술 인용 색인 SCOPUS(https://scopus.com)에서 수학 교과의 자동 채점을 다룬 연구를 수집하고, PRISMA 지침(Liberati et al., 2009; Page et al., 2021)에 따라 문헌을 선정하였다([그림 2] 참고). 수학 분야의 자동 채점이 비교적 최근에 본격적으로 주목받기 시작한 만큼 SCI 등재 논문에 한정하여 분석하기에는 연구의 수가 부족하였고, 분석 대상 연구를 확보하기 위해 수집 범위를 SCOPUS로 확장하였다. 첫째, 검색을 위한 논문 범위와 핵심 키워드를 선정하였다. 논문을 검색하기 위한 키워드로는 수학 교과의 자동 채점으로 번역될 수 있는 검색어를 조합하여 사용하였다. 검색어로는 자동을 의미하는 ‘automated’, ‘automatic’, ‘computerized’와 채점 또는 평가를 뜻하는 ‘scoring’, ‘assessment’, ‘evaluation’, ‘grading’을 조합하였고, 수학 교과에 한정하기 위해 ‘mathematics’를 추가하였다. 단, 2024년 이후에 발표된 논문은 이번 연구에서는 포함하지 않았다. 그 결과 15개 학술지에 게재된 문헌 총 2,501건을 얻을 수 있었다. 해당 키워드로 논문을 검색하는 과정에서 ‘open-ended’, ‘constructed’, ‘descriptive’ 등 구성형 문항과 관련이 있는 연구를 추렸다. 둘째, 중복된 연구 548건을 제외한 1,953건에 대해 영문으로 작성되지 않았거나 학술지 논문 및 학술대회 발표 연구가 아닌 연구, 제목과 초록으로부터 본 연구의 주제와 관련이 없는 연구인지 확인하여 추가로 1,835건을 제외하였다. 셋째, 제외되지 않은 118건의 연구에 대해 원문을 분석하는 과정에서 원문을 얻을 수 없었던 6건 외의 112건의 연구 원문을 분석하여 실증 연구가 아닌 30건, 자동 채점을 수행하고 성능을 분석하는 주제가 아닌 61건을 추가로 제외한 21건의 연구를 최종 분석 대상으로 선정하였다.
자동 채점 연구를 분석하기 위해 본 연구에서는 Zhai 외(2021)의 연구가 제시한 기준을 조정하였다. 이들은 기계학습을 이용한 과학 교과의 자동 채점에서 기계와 인간의 채점 일치도에 영향을 미치는 요소로 기계학습 알고리즘, 문항의 주제 영역, 평가의 형식, 문항의 구성, 학교급, 기계학습의 종류 등 6개의 요소를 제안하였다. STEM 분야에서 수학과 과학 교과는 밀접한 관련이 있기에 수학 교과의 자동 채점 연구 분석 과정에도 타당한 분석 기준으로 볼 수 있다.
본 연구는 기본적인 기준과 함께 연구 대상 학교급, 문항의 구체적인 주제 영역, 채점 방법, 인공지능 모델(알고리즘) 및 기계학습의 종류 등을 기준으로 설정하고, 앞에서 제안한 분석 기준을 종합하여 분석 틀을 구축하였다. 특히 채점 방법은 상술한 대로, 총체적 분석법은 이분형과 다분형, 분석적 채점법은 요소형과 단계형으로 세분화하여 분석하였다. 또한, 분석한 연구들에 사용된 수학 구성형 답안의 종류에 따라 문장형, 수식형, 그래픽형으로 구분하고, 답안의 입력 유형에 따라 손글씨 유형과 디지털 유형으로 구분하였다.
이상의 분석 틀을 종합한 내용은 다음 <표 2>로 정리하였다. 이 분석 기준은 상호 배타적으로 구분된 기준은 아니므로 분석한 연구 중에는 여러 기준을 동시에 만족하는 연구들도 있었으며, 이 경우 각 항목을 중복으로 코딩하였다. 이 분석 기준은 구성형 답안의 자동 채점 연구를 채점 방법 및 답안의 형태에 따라 분류하고자 하는 시도로써 유용한 접근일 수 있다.
IV. 연구 결과
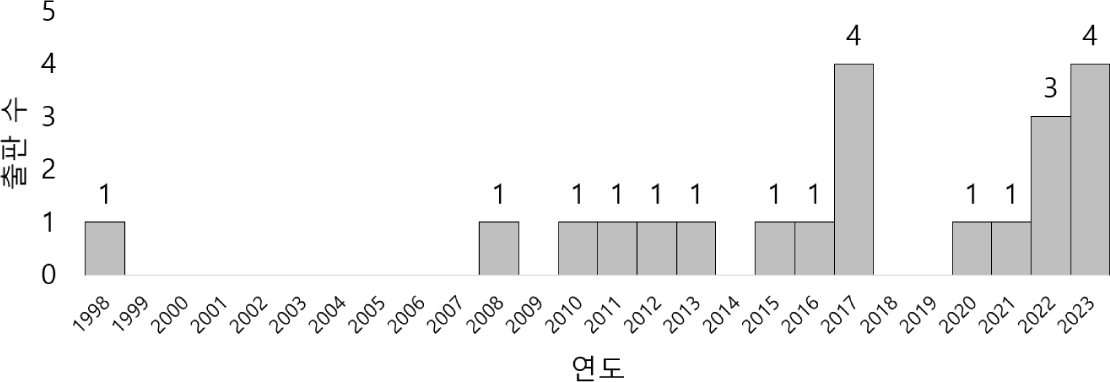
본 절에서는 SCOPUS에서 검색된 수학 자동 채점 연구 문헌을 요약 및 종합하였고, 그 결과는 <표 A1>과 같다. 먼저 일반적인 체계적 문헌 고찰에서 기본적으로 분석하는 출판 연도를 분석하면 [그림 3]과 같다. Singley & Bennett(1998)의 보고서, Tvarožek 외(2008)의 연구와 같은 선구적 논문이 2000년대까지 간헐적으로 있었으나 연구 대부분은 2010년대 이후에 보고되었다. 다만 2017년의 연구 중 3건(Wijesinghe et al., 2017; Wijeweera et al., 2017; Mendis et al., 2017)과 2022년의 연구 중 2건(Baral et al., 2022; Rivera-Bergollo et al., 2022)은 저자의 상당수가 겹치고 비슷한 주제 또는 동일 학생 데이터를 다룬 연구로, 2010년도 후반에야 자동 채점에 관한 연구가 본격화되었다. 실제로 5년 간격의 연구 논문의 수를 정리해보면 2005년까지 1편, 2006년에서 2010년에 2편, 2011년부터 2015년까지 4편이었고, 2016년부터 2020년까지는 6편, 2021년부터 2023년까지는 벌써 8편의 연구가 진행되는 등 점차 연구가 늘고 있다.
게재 학술지를 살펴보면 Artificial Intelligence in Education(AIED)에 2편, International Conference on Educational Data Mining(EDM)에 2편, International Conference on Learning Analytics & Knowledge(LAK)와 ACM Conference on Learning at Scale(L@S)에 각 1편을 포함하여 15개 학술지에 연구가 실렸다. 그러나 분석한 연구의 대부분은 학술대회 발표 자료(proceeding)였고, 나머지 연구 중에서 Singley & Bennett(1998), Fife(2013)의 ETS report series 2편을 제외한 전통적 학술 논문은 TOJET, INASS, ITC, Computers, AIED 등의 학술지에 실린 5편(Yang et al., 2011; Yuhana et al., 2022; Chaowicharat et al., 2023; Nakamoto et al., 2023; Botelho et al., 2023)에 불과했다.
분석한 연구의 대상 학교급과 교과 주제 영역을 정리하면 <표 3>1)과 같다. 연구 결과 주목할 만한 특징 중 하나는 중・고등학생의 답안에 관한 연구가 대부분이라는 점이다. 비록 연구의 대상이 된 학교급이 명시되지 않아 파악할 수 없었거나 여러 학교급을 대상으로 한 연구가 8편 있었으나, 이를 제외한 연구 중 절반 이상(10편)의 연구가 중・고등학교 수준의 연구였다. Tvarožek 외(2008)는 개발한 자동 채점시스템을 중학교 수학에 적용한 뒤 그 확장 가능성을 논하였고, Wijeweera 외(2017), Mendis 외(2017)는 고등학교 기하 문제의 답안에 점수를 부여하는 시스템을 제안하였다. 그 외의 학교급 대상 연구로는 초등학생 대상의 자동 채점 연구(Yang et al., 2011; Yuhana et al., 2022; Asakura et al., 2023) 또는 대학생으로부터 얻은 답안 데이터로 수식의 동등성을 검증한 연구(Nguyen et al., 2012)가 보고되었다.
| 학교급 주제 영역 | 합계 | 수와 연산 | 도형과 측정 | 변화와 관계 | 자료와 가능성 | 비식별 |
|---|---|---|---|---|---|---|
| 합계 | 총 N=21 | 4 | 2 | 8 | 1 | 6 |
| 초등학교급 | 3 | 2 | 1 | |||
| 중고등학교급 | 10 | 1 | 2 | 5 | 1 | 1 |
| 대학교급 이상 | 2 | 2 | ||||
| 비식별 | 7 | 1 | 2 | 4 |
자동 채점 연구의 대부분이 변화와 관계(21편 중 8편) 또는 수와 연산(21편 중 4편)과 같이 기본적인 연산이나 방정식 풀이 과정의 인식 및 채점을 다루었다는 점도 중요한 특징이다. 변화와 관계 영역에서 Othman 외(2010)는 일차방정식 문항의 답안을 자동 채점하는 정보 검색 기반 채점 엔진의 정확도를 보고하였고, Rivera-Bergollo 외(2022)는 로그 방정식의 풀이 및 과정 설명 문항을 사용하였으며, Nguyen 외(2012)는 다양한 함수 표현의 수학적 동등성을 검증하는 알고리즘을 이용해 답안을 검증하였다. 한편 사칙연산과 혼합 계산 답안의 인식률을 분석한 Yuhana 외(2023)의 연구는 수와 연산 영역에서의 자동 채점을 다루었다. 그 외의 영역에서도 작도 문제의 이미지 답안 채점 연구(Wijeweera et al., 2017)나 벤다이어그램 형태의 답안을 채점하는 연구(Wijesinghe et al., 2017) 등 수식 외의 형태로 개방형 답안을 채점하는 연구가 있었으나, 본 연구에서 분석한 논문 중에서는 도형과 측정 영역 2편과 자료와 가능성 영역 1편뿐이었다.
다만 연구 대상이 된 학교급을 파악할 수 없었던 연구가 7편, 명시되지 않은 여러 주제 영역이 혼재되어 구분할 수 없었던 연구가 6편 발견되었는데, 대부분 온라인 플랫폼에서 얻은 대량의 학생 답안 데이터를 사용한 경우로 플랫폼 특성상 특정 학교급이나 주제 영역으로 구분하지 않은 연구라는 특징이 있다(Erickson et al., 2020; Baral et al., 2021; Baral et al., 2022; Botelho et al., 2023).
분석한 연구들 대부분이 채점 모델의 평가를 위한 테스트 데이터의 개수 정도만 제시하였기에, 연구에 사용된 학생의 채점 답안 개수를 기준으로 구분할 때에는 채점 답안 개수의 범위로 구분하여 <표 4>에 정리하였다. 다만 모델의 학습을 위해 전체 데이터를 어떻게 훈련 데이터와 테스트 데이터로 나누었는지 명시한 연구가 3편 있었는데(Kadupitiya et al., 2016; Yuhana et al., 2022; Nakamoto et al., 2023), 특히 Nakamoto 외(2023)는 2,200여 개의 답안을 각각 1,420개의 학습 데이터, 355개의 검증 데이터, 431개의 테스트 데이터로 구분하여 훈련과 검증의 과정을 거쳤다고 구체적으로 설명하였다. 그 밖에도 실제 답안 데이터와 유사한 데이터를 보조로 사용하거나(Rivera-Bergollo et al., 2022) 인공지능으로 잘못 인식된 기호 및 표현을 수정하는 방법(Chaowicharat & Dejdumrong, 2023), 생성형 인공지능을 사용하여 채점 데이터의 부족을 보완하는 방법(Nakamoto et al., 2023)을 제안한 연구도 있었다.
| 데이터 개수 | ~100 | 100~1,000 | 1,000~10,000 | 10,000~ |
|---|---|---|---|---|
| 출판 수 | 5 | 8 | 3 | 5 |
자동 채점을 위해 사용된 알고리즘은 크게 전통적인 규칙 기반의 채점, 초기 기계학습 이론을 바탕으로 한 통계 처리 기반의 채점, 신경망과 트랜스포머 등을 활용한 딥러닝 기반의 채점으로 구분할 수 있다. 초기 자동 채점 연구는 문항의 채점 규칙이나 채점 엔진을 자체적으로 개발하고 적용한 연구가 대부분이었다. CAS(Computer Algebra System) 기반의 PEV(Probablistic Equivalence Verification) 알고리즘 및 SCCS(Stepwise Correctness Checking and Scoring) 기법 등으로 답안에서 수식의 동등성을 확인하거나, m-rater로 채점하는 방식(Singley & Bennett, 1998; Nguyen et al., 2012; Fife, 2013; Othman & Bakar, 2017)을 예로 들 수 있다.
이후 기계학습을 활용한 채점 모델이 도입되면서 채점된 데이터로 채점 모델을 학습시키고 그 성능을 확인하는 연구가 이루어졌다. Lan 외(2015)는 수학적 언어 처리 방법으로 학생 116명의 답안을 유사성 기반 군집화 및 비모수적 베이지안 군집화하여 채점하는 비지도학습 기반의 연구에서 평균절대오차를 채점 모델의 성능 지표로 사용하였고, Yuhana 외(2022)는 학생의 답안에서 연산자와 계산 결과를 분류 및 변환하는 지도학습 기반의 채점 연구에서 랜덤 포레스트, SVM 등으로 사칙계산 및 혼합 계산의 인식 정확도를 분석하였다.
2020년대에 들어서는 딥러닝과 트랜스포머 모델의 연구사례가 주를 이루고 있다. CNN으로 6,000개의 손글씨 이미지를 인식하여 잘못 인식된 기호를 대체하는 방법을 다룬 Chaowicharat & Dejdumrong(2023)의 연구나 디지털 워크북에 손으로 쓴 23,000여 개의 학생 답안을 인식하여 채점하는 bi-LSTM 기반 딥러닝 모델을 제안한 Asakura 외(2023)의 연구가 대표적 사례로, 두 연구 모두 성능 지표로 0.89 이상의 높은 F1-score 값을 얻었다. 특히 전통적인 지도학습 방법들과 LSTM 모델의 채점 성능을 비교한 Erickson 외(2020)의 연구는 150,000건이 넘는 학생 답안 데이터의 자동 채점 결과를 분석하였는데, 이후 같은 데이터에 대하여 여러 모델을 적용하는 연구들(Baral et al., 2021; Rivera-Bergollo et al., 2022; Botelho et al., 2023; Baral et al., 2022)로 연속성 있게 이루어졌다. 특히 연속적인 연구 간의 성능 개선을 비교하기 위해 AUC, RMSE, 다중 클래스 Cohen’s kappa 등 다양한 벤치마크 지표가 공통으로 사용되었다.
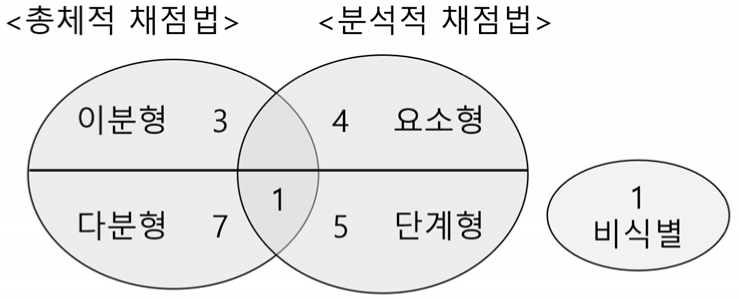
각 연구의 자동 채점 모델이 사용한 채점 방법을 정리하면 [그림 4]와 같다. 총체적 채점법으로 자동 채점한 11편의 연구 중 3편의 연구(Tvarožek et al., 2008; Nguyen et al., 2012; Asakura et al., 2023)는 학생 답안이 모범 답안과 일치하는지를 이분형으로 확인하였다. 그와 달리 학생의 문제 풀이 과정 설명에 대한 점수를 할당하는 예측 모델 연구(Nakamoto et al., 2023)나, 대량의 ASSISTments 학생 답안을 이용한 연구들(Erickson et al., 2020; Baral et al., 2021; Baral et al., 2022; Rivera-Bergollo et al., 2022; Botelho et al., 2023)은 다분형 예측 모델을 사용하였다.
한편 10편의 연구가 분석적 채점법으로 자동 채점한 결과를 보고했는데, 그중 요소형 분석적 채점법을 사용한 연구와 단계형 분석적 채점법을 사용한 연구가 각각 5편이었다. 예를 들어 Singley & Bennett(1998)은 문장제 문항의 학생 답안 채점을 위해 문제 조건(constraint)들의 위배를 각각 확인하는 방식의 분석적 채점법을 제안하였고, Othman & Bakar(2010)는 방정식 풀이 과정을 단계적으로 확인하며 정량적 피드백을 제공하는 기법을 제시하였다. 또, Lan 외(2015)는 답안의 수식 전개 과정을 따라가며 단계별로 수식 답안의 예상점수를 보여주는 모델을 연구하였다. 특히, 총체적 채점법과 분석적 채점법을 모두 적용한 Chaowicharat & Dejdumrong(2023)의 연구는 이미지 인식과 기호 대체의 과정을 거친 수식의 동등성을 채점하는 모델의 평가를 위해 두 방법을 비교했다는 점에서 중요한 의미가 있다.
단, 학생의 답안에서 오류를 식별하는 데에 초점을 맞춘 Yang 외(2011)의 연구는 구체적인 채점 방법을 명시한 대신 발생한 오류와 학생의 수학적 능력 간의 상관관계 분석에 더 집중하였다.
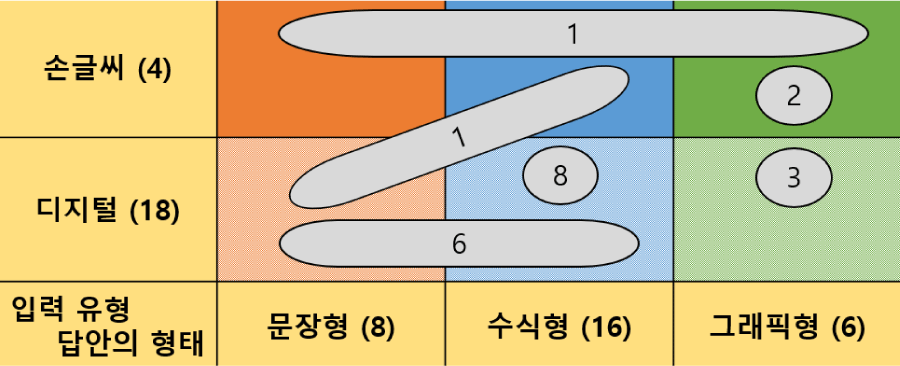
마지막으로 문항 답안의 형태와 입력 유형에 따라 연구를 분석한 결과를 시각화하여 나타내면 [그림 5]와 같다. [그림 5]에서 도형 내의 숫자는 해당 조합에 해당하는 연구의 개수를, 여러 영역에 걸쳐 있는 도형은 도형이 걸쳐 있는 영역에 해당하는 종류의 답안 또는 입력 유형이 모두 다루어진 연구를 의미한다. 이를 통해 알 수 있는 사실은 다음과 같다.
첫째, 분석한 연구 중 문장형 답안을 자동 채점한 연구는 8편 모두 수식형 답안도 함께 자동 채점한 연구였다. 특히, 여러 문항 중 문장형 답안을 요구하는 문항과 수식형 답안을 요구하는 문항이 따로 구성된 2편의 연구(Tvarožek et al., 2008; Asakura et al., 2023)를 제외한 6편의 연구는 모두 하나의 답안에서 문장형과 수식형 표현을 모두 인식하여 자동 채점하는 연구였다. Nakamoto 외(2023)는 학생의 수식형 답안과 풀이 과정을 설명한 문장형 답안을 함께 채점하였고, 다른 연구들도 후술할 바와 같이 문장형과 수식형 답안을 함께 채점하였다. 반면, Tvarožek 외(2008)는 문항반응이론을 바탕으로 자동 채점 결과를 사용하여 학생들에게 다음 문항을 제공하는 시스템을 개발하였다. 문항에 따라 요구되는 답안의 형태가 다를 뿐 개별 문항은 각각 하나의 형태로 입력하는 방식이기는 하나, 문장형과 수식형 응답뿐만 아니라 그래픽 응답까지도 채점하는 단초를 제공한 중요한 연구였다. Asakura 외(2023)도 간단히나마 비슷하게 답안 이미지에서 문장형, 수식형 답안을 인식하여 자동 채점할 때, 동시에 단순한 그림이나 도식 답안을 정답과 비교하는 방법을 시도하였다.
둘째, 수식형 답안의 자동 채점을 포함한 연구는 16편(76.2%)으로 본 연구에서 제안한 분석 틀로 분류한 답안의 형태 중에 가장 많았다. 이 중에서는 수식형 답안만 채점한 연구가 8편, 수식형과 문장형이 혼합된 답안을 채점한 연구가 8편으로 대부분의 자동 채점 연구가 수식형 답안을 대상으로 함을 알 수 있다. 수식형 답안만을 자동 채점한 연구로는 수식의 대수적 동등성을 감지하는 알고리즘을 이용한 연구(Singley & Bennett, 1998; Nguyen et al., 2012; Othman & Bakar, 2017)가 대표적인 예다. 이와 달리 Nakamoto 외(2023)의 연구나, ASSISTments의 데이터를 이용한 연구들(Erickson et al., 2020; Baral et al., 2021; Baral et al., 2022; Rivera-Bergollo et al., 2022; Botelho et al., 2023)은 기본적으로는 문장 형태지만, 연구에서 밝힌 것처럼 “I multiply –3 and 2x”, “Yes Because Y=mx+b”와 같이 디지털 문자로 표현된 수식이 함께 채점되는 멀티모달 답안이었다. 또한, 심층 신경망 모델을 사용하여 수학과 영어, 일본어 인식기를 구축해 화면에 표현된 펜의 궤적과 이미지로 답안을 인식한 연구(Asakura et al., 2023)도 있었다.
셋째, 그래픽형 답안의 자동 채점 연구는 다른 형태와의 혼합 없이 그래픽형 답안만 채점한 연구가 대부분이었다. 앞서 언급한 Asakura 외(2023)의 연구만 유일하게 여러 형태의 답안을 자동 채점한 연구로 분류되었으나, 이조차도 멀티모달 답안의 자동 채점을 다룬 것이 아니라 연구에서 수집한 문항 응답 데이터 중 그래픽형 응답만을 요구하는 문항의 존재로 인해 그래픽형으로 중복코딩된 연구였다. 결과적으로 본 연구에서 분석한 그래픽형 답안을 자동 채점하는 연구 중에 다른 형태가 혼합된 답안을 함께 인식하여 자동채점한 연구는 없었다.
넷째, 손글씨 답안을 채점한 연구(4편)는 디지털 유형의 답안 채점 연구(18편)보다 훨씬 적었다. 특히, 손글씨 답안 채점 연구는 모두 2022년 이후에 출판되었는데, 손글씨 답안의 자동 채점 성능에는 기본적으로 이미지 인식 기술의 성능이 영향을 미친다는 점이 그 이유로 보인다. 이와 관련하여 오인식된 기호를 수정하여 자동 채점의 성능을 개선하거나(Chaowicharat & Dejdumrong, 2023), 펜의 궤적과 최종 답안 이미지 모두를 사용하는 방식(Asakura et al., 2023), 학습자가 자신의 풀이 과정을 설명한 답안을 채점에 사용하는 아이디어(Nakamoto et al., 2023) 등 손글씨 답안의 자동 채점 성능 개선을 위해 여러 방안이 제안되었음을 확인하였다.
V. 논의 및 결론
먼저 주목할 점은 수학 교과의 자동 채점 연구는 대부분 학술대회의 발표 자료이자 채점 기술을 적용한 모델의 성능 확인 연구였다는 점이다. 상술한 대로 최근 들어 전통적인 형태의 학술지 논문도 나오고 있으나, 학술대회의 발표 자료에 비하면 다소 부족하다. 이는 기계학습 및 인공지능 분야의 연구 결과 보고가 주로 학술대회의 발표 자료 형태로 이루어진다는 특징이 반영된 것으로 볼 수 있겠으나, 수학교육 분야에서 자동 채점 연구가 더욱 체계적으로 분석되고 후속 연구가 활발히 이루어지기 위해서는 학술지 논문으로도 많이 출판될 필요가 있다.
연구 대상으로는 중・고등학교급 대상이 많았고, 세부 영역으로는 변화와 관계, 수와 연산처럼 수식 위주 답안 대상의 연구가 많았다. 중・고등학교를 넘는 수준의 수학 답안을 채점하려면 인공지능의 수리논리 능력이 더욱 요구되는데, 이를 구현하기는 더 어렵다. 비슷한 맥락에서 자동 채점 연구가 다룬 영역을 보면, 함수나 방정식, 연산과 관련된 영역에서는 여러 연구가 수행되었으나 다이어그램이나 그래프, 기하학 분야의 답안 자동 채점 연구는 제한적으로 이루어졌다. 수학의 다양한 영역에는 각각 문제해결을 위한 고유의 규칙과 방법, 영역 특정 지식이 있다(Rane, 2023)는 점에서 볼 때, 이는 Maple이나 Mathematica와 같은 CAS 알고리즘 기술의 발전이 있었기 때문이라고 볼 수 있다(Blyth & Labovic, 2004; Olenev et al., 2020).
앞의 논의를 종합하면, 채점 대상 답안의 이해와 자동 채점을 위해서는 여러 수학적 영역에서의 기반 지식을 통한 인공지능의 수리논리 능력 강화가 필요하며(Rane, 2023), 답안으로부터 수학적 중요도가 높은 요소에 주목하여 채점하는 등(최인용 외, 2024) 자동 채점의 성능 개선을 얻을 수 있을 것이다. 엄밀성과 논리라는 수학의 특징 때문에 수학 분야에서 인공지능의 수준 향상이 도전적으로 여겨졌으나, 인간 수준의 추론을 해내는 인공지능 모델이 점차 등장하고 있다(Zheng et al., 2021; Trinh et al., 2024).
한편, 최근 언어모델을 이용한 연구들은 성능 개선을 위해 다양한 프롬프트 엔지니어링 방법을 제안하는데, 이를 통해 인공지능의 수학적 추론 능력을 개선할 수도 있다. 예컨대 CoT(Chain of Thought)나 ToT(Tree of Thought) 기법은 복잡한 추론을 수행하는 언어모델의 성능을 향상시킬 수 있다(Wei et al., 2022; Kojima et al., 2022; Yao et al., 2024; 신병철 외, 2024). 이러한 접근을 발판 삼아, 다양한 수학 영역에서 자동 채점의 도입을 이루어야 할 것이다.
본 연구에서 분석한 자동 채점 연구들은 통상의 기계학습 분야에서 사용하는 것보다 적은 데이터로 모델 학습 및 평가가 이루어졌고, 채점 모델의 학습 과정이나 모델 학습 및 평가에 사용된 데이터의 개수가 구체적으로 제시된 것이 많지 않았는데 이는 학습자의 실제 답안을 분석한 연구라는 특징 때문일 수 있다. 그러나 기계학습이나 딥러닝에서 학습 데이터와 검증 데이터의 개수는 일반적으로 중요한 요소이다. 모델 학습에서 충분한 데이터가 사용되지 못한 경우, 채점 모델은 신뢰성 있는 성능을 보여주지 못하며, 알고리즘 혐오로 불리는 신뢰 문제를 초래할 수 있다(Hsu et al., 2021; Schneider et al., 2023). 자동 채점이 보편적으로 사용되려면 앞으로의 자동 채점 연구에서 고품질의 데이터를 많이 확보하고, 모델 학습에 사용한 데이터의 개수나 품질을 함께 보고하는 것이 필요하다. 그러나 현장에서는 문항 출제 및 채점의 어려움 등의 이유로 채점 모델 학습에 좋은 구성형 문항의 데이터를 많이 얻는 것이 어렵기에, 이러한 한계의 극복 방안을 모색해야 한다. 이와 관련하여 본 연구의 분석 대상 연구들로부터 데이터 확보 문제해결을 위한 여러 방법을 확인하였는데, 특히 생성형 인공지능을 활용한 데이터 증강이 주목할 만하다(Rivera-Bergollo et al., 2022; Chaowicharat & Dejdumrong, 2023; Nakamoto et al., 2023).
인공지능 모델의 발전에 따라 자동 채점 연구에서 사용하는 채점 모델이 변한 점도 확인하였다. 초기 규칙 기반 알고리즘부터 최근의 트랜스포머 기반 언어모델에 이르기까지의 변화는 채점 모델의 성능과 신뢰성 향상을 이루고 있다. 일반적인 인공지능 분야에서 성능과 신뢰성 향상을 위해 여러 시도가 이루어지는 만큼 최신 기술 동향을 계속해서 따라가는 연구가 필요할 것이다.
또한, 분석한 연구들은 대부분 정확도(accuracy)를 채점 모델의 성능으로 제시하고 있었다. 그러나 이를 통해 여러 연구에서 보고된 채점 모델 간의 성능을 단순히 비교하기는 어렵다. 같은 채점 알고리즘을 사용하더라도 각 연구에서 사용한 문항이 달라 보고된 채점 성능에 차이가 생길 수 있기 때문이다. 따라서 자동 채점 연구에서는 채점 모델의 평가 성능을 지표로 제시할 때에도 교육학적으로 더 의미 있는 방식을 취할 필요가 있다. 이에 대해 ASSISTments의 대규모 데이터를 이용한 연구들(Erickson et al., 2020; Baral et al., 2021; Baral et al., 2022; Rivera-Bergollo et al., 2022; Botelho et al., 2023)은 공학적인 접근을 시도했는데, 벤치마크 데이터를 설정한 뒤 선행 연구의 모델 성능 지표인 AUC, RMSE, 다중 클래스 카파 등을 공통으로 사용함으로써 모델의 성능 개선을 직접 비교하였다. 대량의 학습자 답안에 대한 채점 모델의 성능 개선 여부를 분석한 방법이었기에 앞으로의 자동 채점 연구의 보고 방식에 관해 중요한 시사점을 주는 연구라 할 수 있다. 벤치마크 데이터가 개방 데이터라는 점에서 개방 데이터를 활용한 채점 모델 개발도 후행 연구가 필요한 분야이며, 답안에서 개인정보가 드러나지 않도록 처리된 대규모 데이터를 확보하는 것의 중요성도 함께 생각해 볼 수 있다.
본 연구에서 제안한 분석 틀의 관점에서 요약하면, 총체적 채점법과 분석적 채점법을 이용한 연구들이 비슷한 비율로 이루어져 왔다. 총체적 채점법의 경우 이분형으로 판단한 연구보다는 다분형으로 판단한 연구가 더 많았고, 분석적 채점법의 경우 요소형 분석적 채점법과 단계형 분석적 채점법이 비슷하게 다루어졌다. 따라서 수학 교과의 자동 채점 연구는 다양한 채점 방법에 걸쳐 이루어지고 있음을 알 수 있다. 추후 연구들도 특정 채점 방법에 치우치는 것이 아니라 다양한 채점 방법에 적용할 수 있는 방향으로 이루어지는 편이 바람직할 것이다. 그런 의미에서 본 연구가 제시한 분석 틀은 여러 모달리티의 채점 방법을 포괄함으로써, 학습자의 학습을 지원하고 피드백을 제공하는 자동 평가 시스템을 설계하는 데에 기여할 수 있을 것이다.
답안의 형태 관점에서 분석 결과를 정리하면 단일 형태의 답안을 채점한 연구가 2010년대 중반까지 이루어졌고, 점차 여러 형태의 답안을 채점하는 연구들로 발전하고 있었다. 문자 외에도 그림 등 다양한 표현 방식을 결합하면 학습자의 개념 이해도를 더 정확하게 평가할 수 있기에(Ryan & Stieff, 2019), 여러 형태의 답안을 자동 채점하는 연구는 평가 개선을 위해 필수적이다. 특히 수학 교과의 구성형 답안은 때로 그림과 그래프에 의존하거나, 수식과 문장이 섞인 형태가 되기도 한다. 따라서 이러한 답안에서 학습자의 이해도를 명확히 파악하려면 개별 문항에 대한 멀티모달 형태의 답안 인식과 채점을 할 수 있어야 한다. 본 연구가 분석한 논문들도 이러한 문제의식으로부터 답안의 다양한 표현에 대한 자동 채점을 시도했으나, 하나의 문항에 대하여서는 답안 형태를 하나로 제한한 연구가 대부분이었다. 그러므로 하나의 문항에 대하여 학습자가 자유롭게 구성형 답안을 작성할 수 있도록 하고, 문장형과 수식형, 그래픽형 등 세 형태가 혼합된 멀티모달 답안을 한 번에 자동 채점할 수 있도록 후속 연구가 이어져야 한다.
딥러닝 기술 발전에 따라 손글씨 답안을 인식하고 채점하는 의미 있는 시도가 점차 이루어지고 있음을 확인한 점도 중요하다. 비록 온라인 기반의 학습 플랫폼을 활용한 수업이 활성화됨에 따라 디지털 형태로 답안을 수집하고 사용할 수 있는 교육 기회가 증가한 것은 사실이나, 여러 교육적 효과 및 편의를 위해 여전히 손글씨 답안이 교실에서 선호되고 있다(Mueller & Oppenheimer, 2014; Gold & Zesch, 2020; Smolinsky et al., 2020). 손으로 쓴 수학적 문장과 기호를 인식하는 것이 매우 실용적이라는 점(Kukreja & Sakshi, 2022)에서 볼 때, 교실 수업 중에 즉각적인 답안의 평가 및 피드백을 위해 손글씨 답안 인식 및 평가 기술의 확보가 중요하다.
수학교육 관점에서 앞의 논의를 종합하면 멀티모달 손글씨 답안 자동 채점 연구는 교실에서의 자동 채점 활용을 위한 핵심 연구 방향이다. 본 연구의 분석 기준에 해당하지는 않았으나, 딥러닝과 이미지 인식의 발전으로 도입된 이미지 분류 모델 CLIP(Contrastive Language-Image Pre-training) 기술(Radford et al., 2021)을 이용한 Baral 외(2023)의 선도적인 연구처럼 이를 구현하기 위한 시도가 이루어지고 있다. 인공지능 기술의 발전 속도가 매우 빨라 멀티모달 손글씨 답안의 자동 채점에 적용할 수 있는 기술도 속속 개발되는 만큼 앞으로의 수학 교과 자동 채점 연구는 학습자의 자유도 높은 구성형 답안 채점을 위해 이를 활용해야 할 것이다.
또한, 수학 교과의 자동 채점 연구를 위한 시사점으로써 본 연구에서 제안한 분석 틀 중 단계형 분석적 채점법에 주목할 만하다. 수학 교과의 특성상 올바른 논리로 문제를 풀어나가도 계산 오류나 실수로 전체 답안이 틀리게 되는 문제가 발생할 수 있다. 교실에서는 부분 점수를 부여함으로써 학생들이 과하게 감점을 받지 않도록 하는 경우가 있는데, 이는 학생이 정답에 이르는 과정을 알고 있음을 채점에 반영하는 것이다(Smolinsky et al., 2020). 이러한 접근 방식은 수학교육에서 평가가 단순히 정답을 확인하는 것을 넘어 과정에 관심을 기울여야 한다는 점을 강조한다. Rønning(2017)이 주장하듯 학생들은 답뿐만 아니라 과정에 대한 피드백을 원하며, 정답 여부만을 채점하는 방식은 학생들에게 ‘정답을 찾기 위한 무작위 사냥(hunting for the answer)’을 하도록 장려하는 것이 될 수 있다. 따라서 자동 채점에서도 답안에서 부정확한 수치나 계산 실수 등을 감지하고, 풀이 과정에도 피드백 제공과 부분 점수를 부여하여 학습자의 학습을 지원해야 한다. 다만 이를 위한 구체적인 채점 기준은 인간 채점자끼리도 의견의 일치를 이루기 어려운 경우가 많으므로 이에 대한 교육적인 논의가 선행되어야 할 것이다.
본 연구에서 직접 분석한 것은 아니지만, 분석 대상 논문 중에 자동 채점을 통한 수학교육적 효과성을 분석한 연구가 거의 없음을 확인한 점도 의미가 있다. 서론에서 밝힌 바와 같이 자동 채점의 궁극적인 목표는 평가 개선을 통한 교육 효과 증진이므로 자동 채점의 수학교육적 효과성을 밝히는 것이 중요하다. 예컨대 학습자의 학습 과정을 환류하고 지원하기 위해 저부담 평가에서 자동 채점을 사용하는 경우, 수업 중에 작성된 답안에 대한 즉각적인 평가 및 피드백을 통해 교육적 효과를 얻을 수 있어야 할 것이다(Hwang & Tu, 2021). 그러나 채점 모델의 우수한 성능이 곧바로 교육적 효과를 담보하지 않기에 자동 채점의 교육적 효과를 분석하고, 학습자의 학습 개선에 사용하는 다양한 방안을 탐색하는 연구도 필요하다. 이를 위하여 자동 채점의 활용 사례나 피드백 생성, 이를 바탕으로 한 수업 개선 등의 시도가 이루어져야 하며, 이러한 시도의 교육적 효과를 분석하고 교실 현장에 어떻게 활용할 것인지에 대한 논의도 필요하다.
최근에는 생성형 인공지능을 활용한 연구가 여러 방면에서 이루어지면서, 자동 채점 연구에서도 새로운 가능성이 확인되고 있다. 본 연구 주제와 관련된 최근 2-3년의 논문 대부분이 생성형 인공지능을 활용하여 인공지능의 추론 능력 개선이나 보조 데이터 생성, 자동 채점의 성능 개선 등의 성과를 보고하였다(Wardat et al., 2023; Nakamoto et al., 2023). 본 연구에서는 분석하지 않았으나 상업적으로 이를 제공하는 시스템도 이미 등장한 만큼, 학교 교육에서도 이러한 시스템을 제공하여 유용한 인공지능 기술이 모두를 위해 사용될 수 있어야 할 것이다.
본 연구는 다음과 같은 한계점을 가지고 있다. 첫째, 수학 교과의 자동 채점을 다룬 실증 연구가 충분히 이루어지지 않아, 체계적 문헌 고찰 과정에서 최종 선정한 논문이 21편뿐이었다. 둘째, 분석한 연구들 대부분이 채점 모델 알고리즘이나 답안 데이터에 관한 정보를 구체적으로 설명하지 않아 정밀한 모델 및 데이터의 파악과 분류가 어려운 면이 있었다. 셋째, 기준에 따른 분석 대상 연구에 한국어로 된 수학 답안의 자동 채점 연구가 포함되지 않아, 국내 수학 자동 채점 연구를 위해서는 이후 한국어 기반 수학 자동 채점 연구를 반영한 분석이 추가로 이루어질 필요가 있다. 앞서 제시한 바와 같이 자동 채점 기술 및 수학교육에서의 함의를 바탕으로 후속 연구들이 더 이루어진 후에, 자동 채점 연구의 방향을 재확인하는 것도 필요할 것이다.
본 연구는 체계적 문헌 고찰 방법을 사용하여 수학 교과 구성형 답안의 자동 채점 연구를 살펴보았다. PRISMA 지침에 따라 SCOPUS에 등재된 15개 학술지의 총 21편의 논문을 분석 대상으로 선정하였고, 이를 기본적인 서지 요소와 연구 대상 및 채점 방법, 채점 데이터와 알고리즘 및 성능, 답안의 형태와 입력 유형 등의 기준으로 분석하였다.
그 결과 수학 교과의 자동 채점 연구보고는 2010년대부터 조금씩 이루어지다가 2010년 후반부터 점차 증가하였고, 중고등학교급을 대상으로 한 변화와 관계, 수와 연산 영역의 채점 연구가 주를 이루었다. 인공지능 기술 발전에 따라 자동 채점 모델도 초기의 규칙 기반 및 통계 기반 모델에서 기계학습, 딥러닝, 대규모 언어모델 등으로 변화했다. 단일 형태의 디지털 입력 답안을 분석한 초창기 자동 채점 연구는 점차 멀티모달 형태와 손글씨 답안을 자동 채점하는 방향으로 발전하고 있다. 이러한 연구 결과를 바탕으로 하여, 수학 교과의 구성형 답안 자동 채점 연구의 중요성과 필요성을 확인하였고, 멀티모달 손글씨 답안의 자동 채점을 구현하는 방향의 연구와 자동 채점의 교육적 효과성을 분석하는 방향의 연구가 필요함을 정리하였다.